
4.等比数列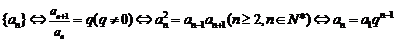 .
.
3.等差数列的性质:①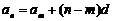 ,
,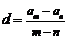 ;
;
②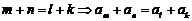 (反之不一定成立);特别地,当
(反之不一定成立);特别地,当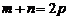 时,有
时,有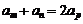 ;
;
③若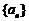 、
、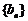 是等差数列,则
是等差数列,则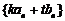 (
(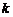 、
、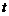 是非零常数)是等差数列;
是非零常数)是等差数列;
④等差数列的“间隔相等的连续等长片断和序列”即 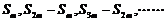 仍是等差数列;
仍是等差数列;
⑤等差数列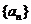 ,当项数为
,当项数为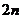 时,
时,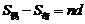 ,
,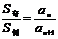 ;项数为
;项数为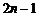 时,
时,
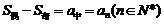 ,
,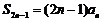 ,且
,且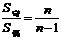 ;
;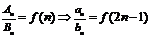 .
.
⑥首项为正(或为负)的递减(或递增)的等差数列前n项和的最大(或最小)问题,转化为解不等式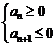 (或
(或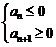 ).也可用
).也可用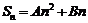 的二次函数关系来分析.
的二次函数关系来分析.
⑦若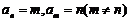 ,则
,则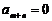 ;若
;若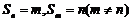 ,则
,则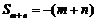 ;
;
若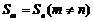 ,则Sm+n=0;S3m=3(S2m-Sm);
,则Sm+n=0;S3m=3(S2m-Sm);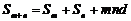 .
.
2.等差数列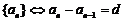 (
(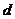 为常数)
为常数)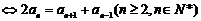
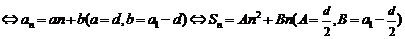 ;
;
1.由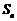 求
求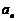 ,
,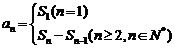 注意验证
注意验证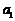 是否包含在后面
是否包含在后面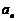 的公式中,若不符合要单独列出.如:数列
的公式中,若不符合要单独列出.如:数列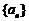 满足
满足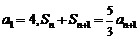 ,求
,求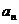 (答:
(答: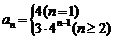 ).
).
5.基本算法语句:
(1)输入语句的格式:INPUT “提示内容”; 变量
(2)输出语句的一般格式:PRINT“提示内容”;表达式,例如:PRINT“S=”;S
(3)赋值语句的一般格式:变量=表达式 作用:赋值语句的作用是将表达式所代表的值赋给变量;

 (4)条件语句
(4)条件语句

 (5)循环语句
(5)循环语句
说明:当型循环又称“前测试型”循环,也就是我们经常讲的“先测试后执行”、“先判断后循环”。
循环结构分为:Ⅰ.当型(while型)--先判断条件,满足则执行循环体,一直到不满足就退出;
Ⅱ.直到型(until型)--先执行一次循环体,再判断条件不满足就循环,直到满足就退出。
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
1.程序框图:


 ①
终端框(起止况);②
输入、输出框;⑥
连接点。
①
终端框(起止况);②
输入、输出框;⑥
连接点。
 ③
③

 处理框(执行框);④
判断框;
⑤ 流程线
;
处理框(执行框);④
判断框;
⑤ 流程线
;
8.算法
7.线性规划
二元一次不等式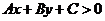 表示
表示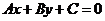 某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。不等式
某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。不等式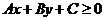 所表示的平面区域边界线画成实线。
所表示的平面区域边界线画成实线。
说明:(1)取一个特殊点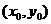 ,从
,从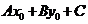 的正负即可判断
的正负即可判断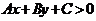 表示直线哪一侧的平面区域。(2)当两个点位于直线
表示直线哪一侧的平面区域。(2)当两个点位于直线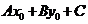 =0两侧,
=0两侧,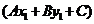
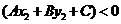 (或
(或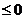 )
)
(3)求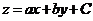 的最大值,将直线
的最大值,将直线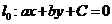 平移正方向服从
平移正方向服从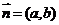 ;
;
(4)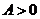
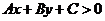 表示直线的右侧;
表示直线的右侧;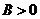
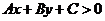 表示直线上方;
表示直线上方;
(5)二元一次不等式表示的平面区域:
①法一:先把二元一次不等式改写成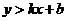 或
或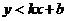 的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断; ②无等号时用虚线表示不包含直线
的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断; ②无等号时用虚线表示不包含直线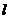 ,有等号时用实线表示包含直线
,有等号时用实线表示包含直线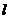 ;
;
③设点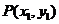 ,
,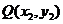 ,若
,若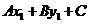 与
与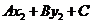 同号,则P,Q在直线
同号,则P,Q在直线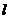 的同侧,异号则在直线
的同侧,异号则在直线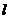 的异侧。如已知点A(-2,4),B(4,2),且直线
的异侧。如已知点A(-2,4),B(4,2),且直线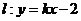 与线段AB恒相交,则
与线段AB恒相交,则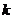 的取值范围是__________
的取值范围是__________
(6)线性规划问题中的有关概念:
①满足关于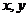 的一次不等式或一次方程的条件叫线性约束条件。
的一次不等式或一次方程的条件叫线性约束条件。
②关于变量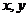 的解析式叫目标函数,关于变量
的解析式叫目标函数,关于变量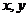 一次式的目标函数叫线性目标函数;
一次式的目标函数叫线性目标函数;
③求目标函数在线性约束条件下的最大值或最小值的问题,称为线性规划问题;
④满足线性约束条件的解(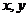 )叫可行解,由所有可行解组成的集合叫做可行域;
)叫可行解,由所有可行解组成的集合叫做可行域;
⑤使目标函数取得最大值或最小值的可行解叫做最优解;
(7)求解线性规划问题的步骤是什么?
①根据实际问题的约束条件列出不等式;②作出可行域,写出目标函数;
③确定目标函数的最优位置,从而获得最优解。
6.(1)一元二次不等式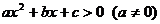 或
或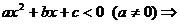 分
分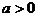 及
及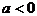 情况分别解之,如设
情况分别解之,如设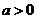 ,
,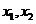 是方程
是方程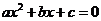 的两实根,且
的两实根,且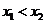 ,则其解集如下表:
,则其解集如下表:
|
|
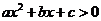 |
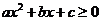 |
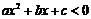 |
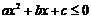 |
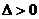 |
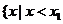 或 或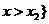 |
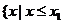 或 或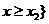 |
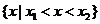 |
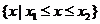 |
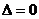 |
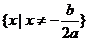 |
R |
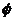 |
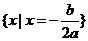 |
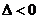 |
R |
R |
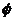 |
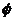 |
如解关于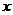 的不等式:
的不等式: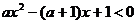 。
。
(2)指数不等式 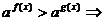
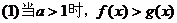 ;
;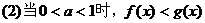 ;
;
对数不等式 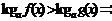 (1)当
(1)当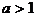 时,
时,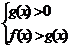 ;(2)当
;(2)当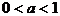 时,
时,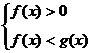 。
。
4.证明不等式常用方法:
⑴比较法:作差比较: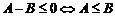 .注意:若两个正数作差比较有困难,可以通过它们的平方差来比较大小;⑵综合法:由因导果;⑶分析法:执果索因.基本步骤:要证…需证…,只需证…; ⑷反证法:正难则反;
.注意:若两个正数作差比较有困难,可以通过它们的平方差来比较大小;⑵综合法:由因导果;⑶分析法:执果索因.基本步骤:要证…需证…,只需证…; ⑷反证法:正难则反;
⑸放缩法:将不等式一侧适当的放大或缩小以达证题目的.
放缩法的方法有:①添加或舍去一些项,如: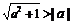 ;
;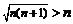 .②将分子或分母放大(或缩小)③利用基本不等式,如:
.②将分子或分母放大(或缩小)③利用基本不等式,如: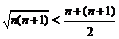 .④利用常用结论:
.④利用常用结论: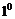
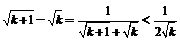 ;
;
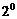
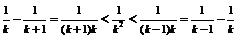 (程度大);
(程度大);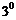
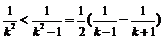 (程度小);
(程度小);
⑹换元法:减少不等式中变量,以使问题化难为易,化繁为简,常用的换元有三角换元、代数换元.
如:知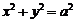 ,可设
,可设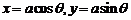 ;
;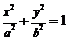 ,可设
,可设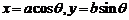 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com