
3.掌握重要不等式,(1)均值不等式:若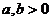 ,则
,则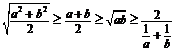 (当且仅当
(当且仅当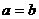 时取等号)使用条件:“一正二定三相等 ”, 常用的方法为:拆、凑、平方等;
时取等号)使用条件:“一正二定三相等 ”, 常用的方法为:拆、凑、平方等;
(2) ,
,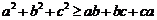 (当且仅当
(当且仅当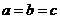 时,取等号);
时,取等号);
(3)公式注意变形如: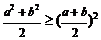 ,
,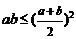 ;若
;若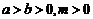 ,则
,则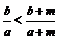 (真分数的性质);
(真分数的性质);
2.掌握几类不等式(一元一次、二次、绝对值不等式、简单的指数、对数不等式)的解法,尤其注意用分类讨论的思想解含参数的不等式;勿忘数轴标根法,零点分区间法.
1.掌握课本上的几个不等式性质,注意使用条件,另外需要特别注意:
①若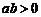 ,
,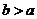 ,则
,则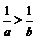 .即不等式两边同号时,不等式两边取倒数,不等号方向要改变.
.即不等式两边同号时,不等式两边取倒数,不等号方向要改变.
②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论.
③取倒数: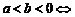
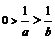 ;
;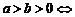
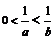 ;如
;如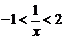 ,等价于
,等价于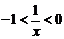 或
或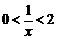
17. 函数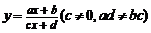 的图像是双曲线:①两渐近线分别直线
的图像是双曲线:①两渐近线分别直线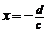 (由分母为零确定)和直线
(由分母为零确定)和直线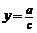 (由分子、分母中
(由分子、分母中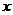 的系数确定);②对称中心是点
的系数确定);②对称中心是点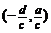 ;③反函数为
;③反函数为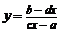 ;
;
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
16.复合函数:⑴复合函数定义域求法:若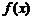 的定义域为
的定义域为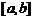 ,其复合函数
,其复合函数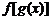 的定义域可由不等式
的定义域可由不等式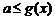
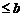 解出;若
解出;若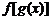 的定义域为
的定义域为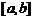 ,求
,求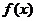 的定义域,相当于
的定义域,相当于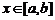 时,求
时,求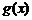 的值域;⑵复合函数的单调性由“同增异减”判定.
的值域;⑵复合函数的单调性由“同增异减”判定.
15.一元二次方程实根分布:先画图再研究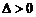 、轴与区间关系、区间端点函数值符号;
、轴与区间关系、区间端点函数值符号;
14.二次函数解析式的三种形式: ①一般式: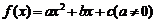 ;②顶点式:
;②顶点式:
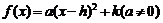 ; ③零点式:
; ③零点式: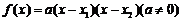 .
.
12.恒成立问题的处理方法:⑴分离参数法(最值法); ⑵转化为一元二次方程根的分布问题;
1).恒成立问题
若不等式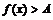 在区间
在区间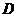 上恒成立,则等价于
;
上恒成立,则等价于
;
若不等式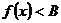 在区间
在区间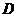 上恒成立,等价于
上恒成立,等价于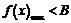 。
。
2).能成立问题
若在区间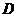 上存在实数
上存在实数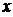 使不等式
使不等式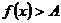 成立,则等价于在区间
成立,则等价于在区间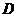 上
上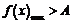 ;
;
若在区间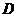 上存在实数
上存在实数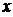 使不等式
使不等式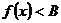 成立,则等价于在区间
成立,则等价于在区间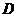 上的
.
上的
.
3).恰成立问题:恒成立最值法,如: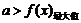 ,则
,则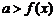 恒成立.
恒成立.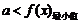 ,则
,则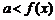 恒成立.
恒成立.
若不等式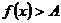 在区间
在区间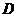 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式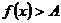 的解集为
的解集为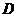 ;若不等式
;若不等式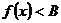 在区间
在区间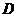 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式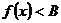 的解集为
的解集为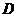 .13.处理二次函数的问题勿忘数形结合;二次函数在闭区间上必有最值,求最值问题用“两看法”:
.13.处理二次函数的问题勿忘数形结合;二次函数在闭区间上必有最值,求最值问题用“两看法”:
一看开口方向;二看对称轴与所给区间的相对位置关系;
11.方程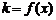 有解
有解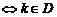 (
(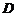 为
为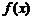 的值域);
的值域);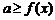 恒成立
恒成立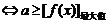 ,
,
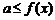 恒成立
恒成立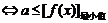 .
.
10.对数:⑴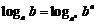
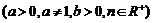 ;
;
⑵对数恒等式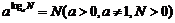 ;
;
⑶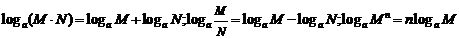 ;
;
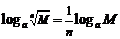 ;⑷对数换底公式
;⑷对数换底公式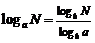
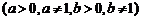 ;
;
推论: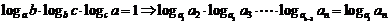 .
.
(以上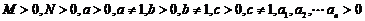 且
且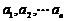 均不等于
均不等于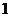 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com