
16.解决直线与圆的关系问题时,要充分发挥圆的平面几何性质的作用(如半径、半弦长、弦心距构成直角三角形,切线长定理、割线定理、弦切角定理等等).
15.过圆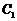 :
: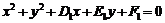 ,
,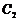 :
: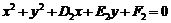 交点的圆(相交弦)系方程为
交点的圆(相交弦)系方程为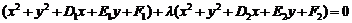 .
.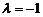 时为两圆相交弦所在直线方程.
时为两圆相交弦所在直线方程.
14.圆与圆的位置关系,经常转化为两圆的圆心距与两圆的半径之间的关系.设两圆的圆心距为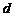 ,两圆的半径分别为
,两圆的半径分别为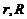 :
: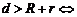 两圆相离;
两圆相离;
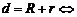 两圆相外切;
两圆相外切; 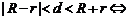 两圆相交;
两圆相交;
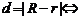 两圆相内切;
两圆相内切; 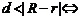 两圆内含;
两圆内含;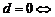 两圆同心.
两圆同心.
9. 圆的方程的求法:⑴待定系数法;⑵几何法;⑶圆系法。
⑴圆的标准方程: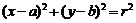 .⑵圆的一般方程:
.⑵圆的一般方程: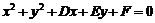
提醒:只有当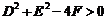 时,方程
时,方程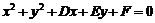 才表示圆心为
才表示圆心为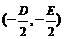 ,半径为
,半径为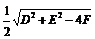 的圆(二元二次方程
的圆(二元二次方程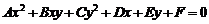 表示圆
表示圆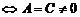 ,且
,且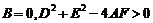 ).
).
⑶圆的参数方程: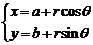 (
(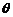 为参数),其中圆心为
为参数),其中圆心为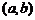 ,半径为
,半径为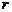 .圆的参数方程主要应用是三角换元:
.圆的参数方程主要应用是三角换元: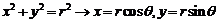 ;
; 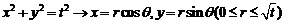 .
.
⑷以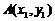 、
、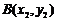 为直径的圆的方程
为直径的圆的方程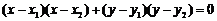 ;
;
10点和圆的位置关系的判断通常用几何法(计算圆心到直线距离).点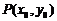 及圆的方程
及圆的方程
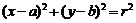 .
.
①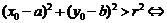 点
点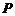 在圆外;②
在圆外;②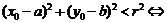 点
点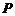 在圆内;
在圆内;
③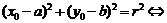 点
点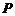 在圆上.
在圆上.
11圆上一点的切线方程:点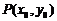 在圆
在圆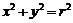 上,则过点
上,则过点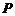 的切线方程为:
的切线方程为: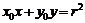 ;
;
过圆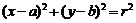 上一点
上一点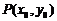 切线方程为
切线方程为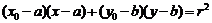 .
.
12过圆外一点作圆的切线,一定有两条,如果只求出了一条,那么另外一条就是与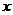 轴垂直的直线.
轴垂直的直线.
13直线与圆的位置关系,通常转化为圆心距与半径的关系,或者利用垂径定理,构造直角三角形解决弦长问题.
①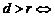 相离 ②
相离 ②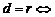 相切 ③
相切 ③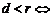 相交
相交
8.有关对称的一些结论
⑴点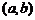 关于
关于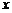 轴、
轴、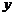 轴、原点、直线
轴、原点、直线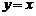 的对称点分别是
的对称点分别是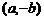 ,
,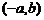 ,
,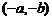 ,
,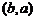 .
.
⑵曲线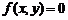 关于下列点和直线对称的曲线方程为:
关于下列点和直线对称的曲线方程为:
①点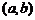 :
: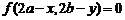 ;②
;②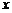 轴:
轴: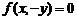 ;
;
③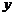 轴:
轴: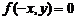 ;
④原点:
;
④原点: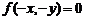 ;
;
⑤直线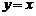 :
: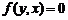 ; ⑥直线
; ⑥直线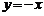 :
: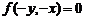 ;
;
⑦直线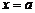 :
: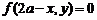 .
.
7.点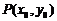 到直线
到直线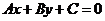 的距离公式
的距离公式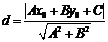 ;
;
两条平行线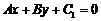 与
与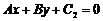 的距离是
的距离是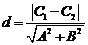 .
.
设三角形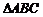 三顶点
三顶点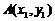 ,
,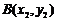 ,
,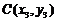 ,则重心
,则重心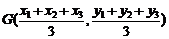 ;
;
6.直线系方程:
①过两直线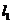 :
: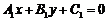 ,
,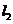 :
: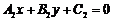 .
.
交点的直线系方程可设为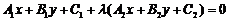 ;
;
②与直线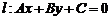 平行的直线系方程可设为
平行的直线系方程可设为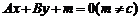 ;
;
③与直线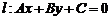 垂直的直线系方程可设为
垂直的直线系方程可设为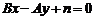 .
.
5.直线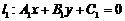 与直线
与直线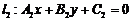 的位置关系:
的位置关系:
⑴平行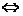
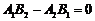 (斜率)且
(斜率)且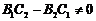 (在
(在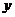 轴上截距);
轴上截距);
⑵相交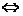
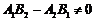 ;(3)重合
;(3)重合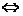
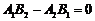 且
且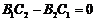 .
.
4.设直线方程的一些常用技巧:
(1)知直线纵截距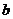 ,常设其方程为
,常设其方程为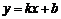 ;
;
(2)知直线横截距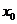 ,常设其方程为
,常设其方程为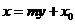 (它不适用于斜率为0的直线);
(它不适用于斜率为0的直线);
(3)知直线过点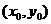 ,当斜率
,当斜率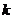 存在时,常设其方程为
存在时,常设其方程为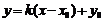 ,当斜率
,当斜率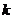 不存在时,则其方程为
不存在时,则其方程为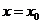 ;
;
(4)与直线 平行的直线可表示为
平行的直线可表示为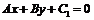 ;
;
(5)与直线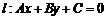 垂直的直线可表示为
垂直的直线可表示为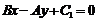 .
.
提醒:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解
3.直线方程五种形式:
⑴点斜式:已知直线过点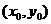 斜率为
斜率为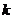 ,则直线方程为
,则直线方程为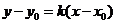 ,它不包括垂直于
,它不包括垂直于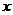 轴的直线.⑵斜截式:已知直线在
轴的直线.⑵斜截式:已知直线在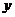 轴上的截距为
轴上的截距为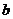 和斜率
和斜率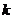 ,则直线方程为
,则直线方程为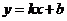 ,它不包括垂直于
,它不包括垂直于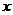 轴的直线. ⑶两点式:已知直线经过
轴的直线. ⑶两点式:已知直线经过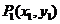 、
、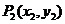 两点,则直线方程为
两点,则直线方程为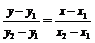 ,它不包括垂直于坐标轴的直线.⑷截距式:已知直线在
,它不包括垂直于坐标轴的直线.⑷截距式:已知直线在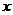 轴和
轴和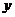 轴上的截距为
轴上的截距为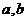 ,则直线方程为
,则直线方程为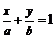 ,它不包括垂直于坐标轴的直线和过原点的直线.⑸一般式:任何直线均可写成
,它不包括垂直于坐标轴的直线和过原点的直线.⑸一般式:任何直线均可写成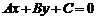 (
(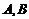 不同时为0)的形式.
不同时为0)的形式.
提醒:⑴直线方程的各种形式都有局限性.(如点斜式不适用于斜率不存在的直线,还有截距式呢?)
⑵直线在坐标轴上的截距可正、可负、也可为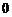 .直线两截距相等
.直线两截距相等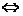 直线的斜率为
直线的斜率为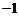 或直线过原点;直线两截距互为相反数
或直线过原点;直线两截距互为相反数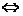 直线的斜率为
直线的斜率为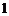 或直线过原点;直线两截距绝对值相等
或直线过原点;直线两截距绝对值相等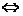 直线的斜率为
直线的斜率为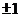 或直线过原点.
或直线过原点.
⑶截距不是距离,截距相等时不要忘了过原点的特殊情形. 直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等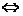 直线的斜率为
或直线过 ;直线两截距互为相反数
直线的斜率为
或直线过 ;直线两截距互为相反数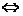 直线的斜率为 或直线过 ;直线两截距绝对值相等
直线的斜率为 或直线过 ;直线两截距绝对值相等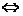 直线的斜率为
或直线过 。
直线的斜率为
或直线过 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com