
17.(本小题满分12分)
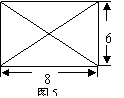 已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视
已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视
图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左
视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积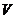 ;
;
(2)求该几何体的侧面积 .
.
7.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为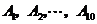 (如
(如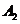 表示身高(单位:cm)在
表示身高(单位:cm)在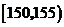 内的学生人数).
内的学生人数).
图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160-180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
A.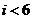 B.
B.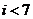 C.
C.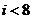 D.
D.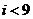
2.在学校应创新条件开设的模块中,各校可根据自身的实际,在已开设的专题外,再选择一些专题开课。建议各校应至少再开设2个专题。
18.设平面直角坐标系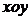 中,设二次函数
中,设二次函数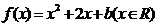 的图像与两坐标轴有三个交点,经过这三个交点的圆记为
的图像与两坐标轴有三个交点,经过这三个交点的圆记为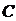 .求:
.求:
(1)求实数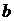 的取值范围;
的取值范围;
(2)求圆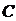 的方程;
的方程;
(3)问圆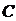 是否经过某定点(其坐标与
是否经过某定点(其坐标与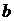 无关)?请证明你的结论.
无关)?请证明你的结论.
17.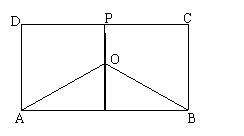 某地有三家工厂,分别位于矩形
某地有三家工厂,分别位于矩形 的顶点
的顶点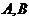 及
及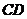 的中点
的中点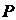 处,已知
处,已知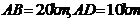 ,为了处理三家工厂的污水,现要在矩形
,为了处理三家工厂的污水,现要在矩形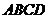 的区域上(含边界),且
的区域上(含边界),且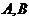 与等距离的一点
与等距离的一点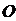 处建造一个污水处理厂,并铺设排污管道
处建造一个污水处理厂,并铺设排污管道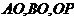 ,设排污管道的总长为
,设排污管道的总长为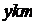 .
.
(1)按下列要求写出函数关系式:
①设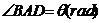 ,将
,将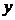 表示成
表示成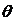 的函数关系式;
的函数关系式;
②设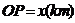 ,将
,将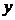 表示成
表示成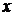 的函数关系式;
的函数关系式;
(2)请你选用(1)中的一个函数关系式,确定污水
处理厂的位置,使三条排污管道总长度最短.
19.(本小题满分14分)
设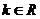 ,函数
,函数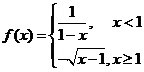 ,
,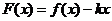 ,
,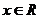 .试讨论函数
.试讨论函数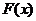 的单调性.
的单调性.
*08江苏卷
18.(本小题满分13分)
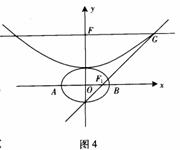 设
设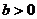 ,椭圆方程为
,椭圆方程为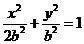 ,抛物线方程
,抛物线方程
为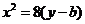 .如图4所示,过点
.如图4所示,过点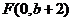
作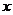 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为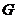 .
.
已知抛物线在点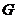 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点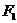 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设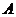 、
、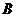 分别是椭圆长轴的左、右端点,试探究在抛物
分别是椭圆长轴的左、右端点,试探究在抛物
线上是否存在点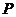 ,使得
,使得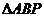 为直角三角形?若存在,请
为直角三角形?若存在,请
指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
2.3.2 探究性试题
*08广东理科卷
19.(本小题满分14分)
如图6所示,等腰三角形△ABC的底边AB=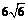 ,高CD=3,点E是线段BD上异于B、D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACEF的体积。
,高CD=3,点E是线段BD上异于B、D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACEF的体积。
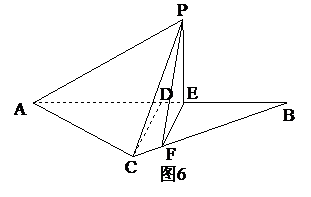 (1)求V(x)的表达式;
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值。
(1)由折起的过程可知,PE⊥平面ABC,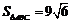 ,
,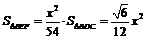
V(x)=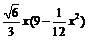 (
(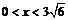 )
)
(2)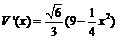 ,所以
,所以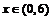 时,
时,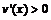 ,V(x)单调递增;
,V(x)单调递增;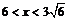 时
时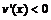 ,V(x)单调递减;因此x=6时,V(x)取得最大值
,V(x)单调递减;因此x=6时,V(x)取得最大值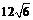 ;
;
(3)过F作MF//AC交AD与M,则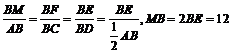 ,PM=
,PM=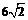 ,
,
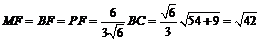 ,
,
在△PFM中, 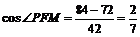 ,∴异面直线AC与PF所成角的余弦值为
,∴异面直线AC与PF所成角的余弦值为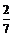 ;
;
是折叠立体的问题,综合了立体几何、函数、导数和极值等知识,思维要求和知识综合度较高,解法多样,较全面地考查了空间想象能力、推理论证能力和运算求解能力,以及创新意识和数学地分析、解决问题的能力。
试卷注重了对抽象概括能力的考查,如文科第21题(理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com