
C.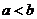 D.
D.
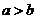
 A.
A.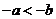 B.
B.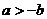
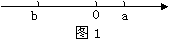
3. 实数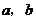 在数轴上的位置如图1所示,则下列各式正确的是( )。
在数轴上的位置如图1所示,则下列各式正确的是( )。




① ② ③ ④
A.①② B。②③ C。③④ D。①④
2. 下列奥运会徽是轴对称图形的是( )
A.(
―2)3与(―3)2 B. ―23与(―2)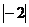
1.下列是互为相反数的一组为
19.(共14分)
解:(Ⅰ)因为,且边通过点,所以所在直线的方程为.
设两点坐标分别为.
由 得.
所以.
又因为边上的高等于原点到直线的距离.
所以,.
(Ⅱ)设所在直线的方程为,
由得.
因为在椭圆上,
所以.
设两点坐标分别为,
则,,
所以.
又因为的长等于点到直线的距离,即.
所以.
所以当时,边最长,(这时)
此时所在直线的方程为.
19.(本小题共14分)
已知的顶点在椭圆上,在直线上,且.
(Ⅰ)当边通过坐标原点时,求的长及的面积;
(Ⅱ)当,且斜边的长最大时,求所在直线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com