
题目列表(包括答案和解析)
1在等比数列{an}中,a2=8,a5=64,,则公比q为( )
A.2 B.3 C.4 D.8
2 已知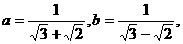 则
则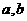 的等差中项为( )
的等差中项为( )
A.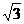 B.
B.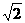 C.
C.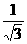 D.
D.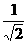
3等比数列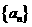 中,
中,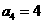 ,则
,则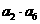 等于( )
等于( )
A.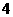 B.
B.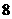 C.
C.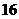 D.
D.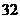
4等差数列{an}的前n项和为Sn,若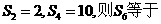 ( )
( )
A.12 B.18 C.24 D.42
5在 中,
中,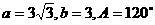 ,则B的值为( )
,则B的值为( )
A、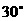 B、
B、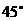 C、
C、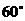 D、
D、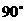
6在⊿ABC中,已知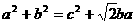 ,则
,则 C=
C=
A 300 B 1500 C 450 D 1350
7在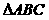 中,已知
中,已知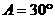 ,
,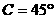 ,
,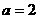 ,则
,则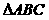 的面积等于( )
的面积等于( )
A.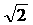 B.
B.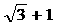 C.
C.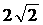 D.
D.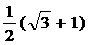
8已知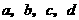 成等比数列,且曲线
成等比数列,且曲线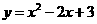 的顶点是
的顶点是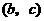 ,则
,则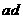 等于( )
等于( )
A.3 B.2 C.1 D.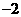
9设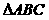 的三内角A、B、C成等差数列,sinA 、sinB、
sinC成等比数列,则这个三角形的形状是( )
的三内角A、B、C成等差数列,sinA 、sinB、
sinC成等比数列,则这个三角形的形状是( )
A.直角三角形 B钝角三角形
C.等腰直角三角形 D.等边三角形
10在不等边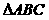 中,a是最大的边,若a
中,a是最大的边,若a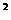 <b
<b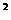 +c
+c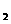 则的取值范围是( )
则的取值范围是( )
A.(90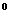 ,180
,180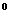 ) B.(45
) B.(45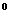 ,90
,90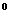 )
)
C.(60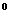 ,90
,90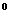 ) D.(0
) D.(0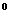 ,90
,90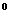 )
)
17题、第Ⅰ小题(7分):已知函数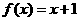 ,设
,设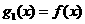 ,
,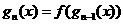
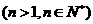 (1)、求
(1)、求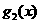 ,
,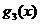 的表达式,并猜想
的表达式,并猜想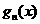
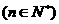 的表达式(直接写出猜想结果) (2)若关于
的表达式(直接写出猜想结果) (2)若关于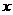 的函数
的函数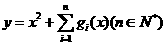 在区间
在区间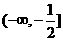 上的最小值为6,求
上的最小值为6,求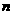 的值。
的值。
第Ⅱ小题(6分):设关于x的不等式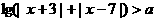
(1)当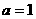 时,解这个不等式;(2)当
时,解这个不等式;(2)当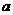 为何值时,这个不等式的解集为R
为何值时,这个不等式的解集为R
18题. 设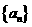 为等比数列,
为等比数列,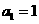 ,
,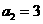 .(1)求最小的自然数
.(1)求最小的自然数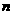 ,使
,使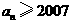 ;
;
(2)求和: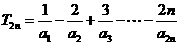 .
.
解:
19题、经过长期观测得到,在交通繁忙的时间段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度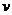 (千米/小时)之间的函数关系式为
(千米/小时)之间的函数关系式为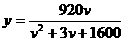 (
(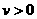 )。(1)在该时段内,当汽车的平均速度
)。(1)在该时段内,当汽车的平均速度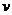 为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时);(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时);(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
解:
20题 已知数列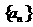 的前
的前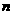 项和为
项和为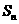 ,且
,且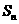 =
=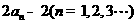 ,数列
,数列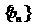 中,
中,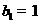 ,点
,点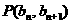 在直线
在直线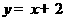 上.(1)求数列
上.(1)求数列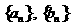 的通项公式
的通项公式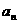 和
和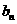 ; (2) 设
; (2) 设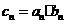 ,求数列
,求数列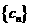 的前n项和
的前n项和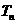 ,并求满足
,并求满足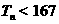 的最大正整数
的最大正整数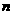 .
.
解
21题.设数列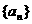 的前
的前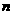 项和为
项和为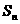 ,且
,且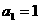 ,
,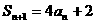 (
(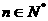 ),
),
(1) 设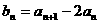 ,求证:数列
,求证:数列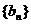 是等比数列;(2)
是等比数列;(2) 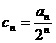 ,求证:数列
,求证:数列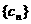 是等差数列; (3) 求
是等差数列; (3) 求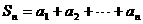 的值。
的值。
15、设集合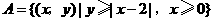 ,
,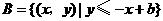 ,,
,,
(1)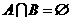
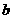 的取值范围是 ;(2)若
的取值范围是 ;(2)若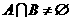 ,
,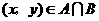 ,且
,且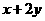 的最大值为9,则
的最大值为9,则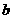 的值是 ___
的值是 ___
14.若在△ABC中,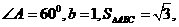 则
则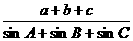 =____________
=____________
13、已知等差数列{an}的公差d≠0,且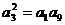 ,则
,则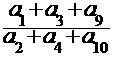 的值是_____
的值是_____
11命题p: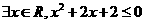 的否定是
的否定是
12、数列{an}的通项公式是a n =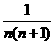 (n∈N*),若前n项的和为
(n∈N*),若前n项的和为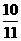 ,则项数为 ____
,则项数为 ____
10.设p:x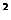 -x-20>0,q:
-x-20>0,q: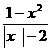 <0,则p是q的( )
<0,则p是q的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
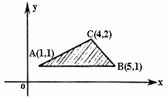
9.在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数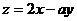 取得最大值的最优解有无数个,则
取得最大值的最优解有无数个,则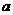 为( )
为( )
A.-2 B.2 C.-6 D.6
8. {an}是等差数列,
{an}是等差数列,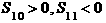 ,则使
,则使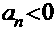 的最小的n值是( )
的最小的n值是( )
A.5
B.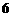 C.7
D.8
C.7
D.8
7.在等比数列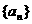 中,公比
中,公比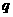 是整数,
是整数,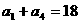 ,
,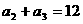 ,则此数列的前8项和为( ) A、514 B、513 C、512 D、510
,则此数列的前8项和为( ) A、514 B、513 C、512 D、510
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com