
题目列表(包括答案和解析)
7. 给出下列结论:
(1)在回归分析中,可用指数系数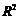 的值判断模型的拟合效果,
的值判断模型的拟合效果,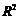 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)在回归分析中,可用相关系数 的值判断模型的拟合效果,
的值判断模型的拟合效果, 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的有( )个.
A.1 B.2 C.3 D.4
4. a=0 是复数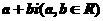 为纯虚数的( )
为纯虚数的( )
(A)充分条件 (B)必要条件
(C)充要条件 (D)非充分非必要条件
5从某大学随机选取8名女大学生,其身高x(cm)和体重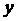 (kg)的回归方程为
(kg)的回归方程为 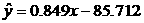 ,则身高172cm的女大学生,由回归方程可以预报其体重 ( )
,则身高172cm的女大学生,由回归方程可以预报其体重 ( )
A.为6 0.316kg B. 约为6 0.316kg
C.大于6 0.316kg D.小于6 0.316kg
6设两个变量x和y之间具有线性相关关系,它们的相关系数是 ,
,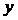 关于
关于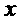 的回归直线的回归系数为
的回归直线的回归系数为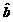 ,回归截距是
,回归截距是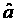 ,那么必有
(
)
,那么必有
(
)
A.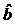 与
与 的符号相同
B.
的符号相同
B. 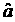 与
与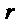 的符号相同
的符号相同
C.
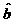 与
与 的符号相反
D.
的符号相反
D. 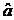 与
与 的符号相反
的符号相反
3.设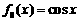 ,
,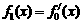 ,
,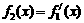 ,…,
,…,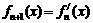 (n∈N),则
(n∈N),则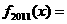 (
).
(
).
A. 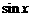 B.
B. 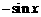 C.
C.  D.
D. 
2.按照下列三种化合物的结构式及分子式的规律,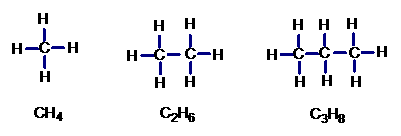
写出后一种化合物的分子式是( ).
A.C4H9 B.C4H10 C.C4H11 D.C6H12
1.复数1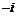 在复平面内对应的点位于(
)
在复平面内对应的点位于(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:设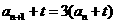 ,则
,则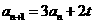 ,
,
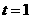 ,
,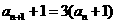
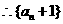 为等比数列,
为等比数列,
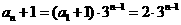 ,
,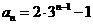 点评:求递推式形如
点评:求递推式形如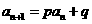 (p、q为常数)的数列通项,可用迭代法或待定系数法构造新数列an+1+
(p、q为常数)的数列通项,可用迭代法或待定系数法构造新数列an+1+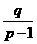 =p(an+
=p(an+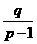 )来求得,也可用“归纳-猜想-证明”法来求,这也是近年高考考得很多的一种题型.练习5已知数列
)来求得,也可用“归纳-猜想-证明”法来求,这也是近年高考考得很多的一种题型.练习5已知数列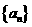 满足
满足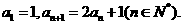 数列
数列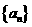 的通项公式是
的通项公式是
小测验一 答案CDDBCA 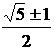
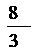
解答题 解:当x=1时,Sn=1+2+3+…+n=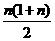 4分
4分
当x≠1时,Sn=1+2x+3x2+…+nxn-1 ①
xSn= x+2x2+…+(n-1) xn-1+nxn ② 4分
①-②: (1-x) Sn=1+x+x2+x3+…+xn-1+nxn
4分
=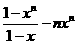 4分
4分
Sn=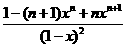 4分
4分
练习1 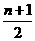 练习2
练习2
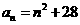
练习3解:由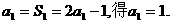
当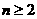 时,有
时,有
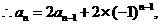
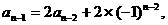 ……,
……,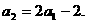
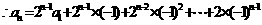
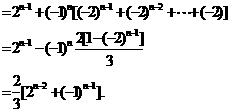
经验证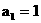 也满足上式,所以
也满足上式,所以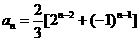
练习4
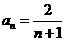 练习5
练习5
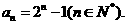
解:由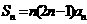 得
得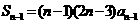
两式相减得: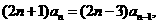 ,
,
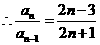 ,
,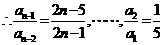
将上面n-1个等式相乘得:
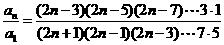
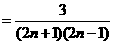
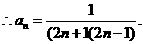
点评:累乘法是反复利用递推关系得到n-1个式子累乘求出通项,这种方法最终转化为求{f(n)}的前n-1项的积,要注意求积的技巧.
练习4.若满足a1=1,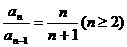 ,
,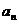 =
=
例4.设数列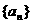 的前n项和为Sn=2n2,求数列
的前n项和为Sn=2n2,求数列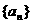 的通项公式;
的通项公式;
解:(1):当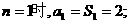
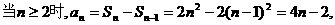
故{an}的通项公式为 的等差数列.点评:利用公式
的等差数列.点评:利用公式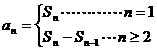 求解时,要注意对n分类讨论,但若能合写时一定要合并.
求解时,要注意对n分类讨论,但若能合写时一定要合并.
练习3已知数列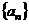 的前
的前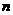 项和
项和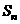 满足
满足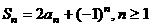 .求数列
.求数列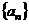 的通项公式;
答案
的通项公式;
答案
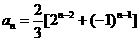
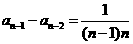 ,……,
,……,
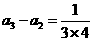 ,
,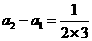 ,
,
以上式子累加,利用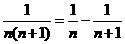 得
得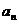 -
-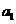 =
=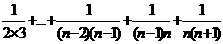
=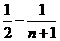 ,
,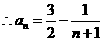 点评:累加法是反复利用递推关系得到n-1个式子累加求出通项,这种方法最终转化为求{f(n)}的前n-1项的和,要注意求和的技巧.练习2已知数列
点评:累加法是反复利用递推关系得到n-1个式子累加求出通项,这种方法最终转化为求{f(n)}的前n-1项的和,要注意求和的技巧.练习2已知数列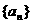 满足
满足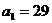 ,
,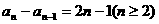 求
求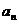
练习1设a1=1,an+1=an+,则an=_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com