
题目列表(包括答案和解析)
1.已知直线a、b、l及平面M、N。给出下列四个命题①若a∥M,b∥M,则a∥b ②若a∥M,b⊥a,则b⊥M ③若a M,b
M,b M,且l⊥a,l⊥b,则l⊥M ④若a⊥M,a∥N,则M⊥N 其中真命题的序号是_____________.(将所有正确结论的序号都写上)
M,且l⊥a,l⊥b,则l⊥M ④若a⊥M,a∥N,则M⊥N 其中真命题的序号是_____________.(将所有正确结论的序号都写上)
14. (Ⅰ)证明:如图,连接
(Ⅰ)证明:如图,连接 与
与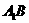 相交于
相交于 。
。
则 为
为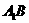 的中点连结
的中点连结 ,又
,又 为
为 的中点
的中点
 又
又 平面
平面
 平面
平面 ……4分
……4分
(Ⅱ) ∴四边形
∴四边形 为正方形
为正方形
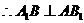 又
又 面
面

 面
面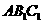 ……6分
……6分
 又在直棱柱
又在直棱柱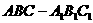 中
中
 平面
平面 。……8分
。……8分
(Ⅲ)当点 为
为 的中点时,平面
的中点时,平面 平面
平面 ……9分
……9分
 、
、 分别为
分别为 、
、 的中点
的中点
 平面
平面
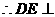 平面
平面 又
又 平面
平面 ∴平面
∴平面 平面
平面 ……12分
……12分
13. 证明:(1)由PA
证明:(1)由PA 平面ABCD
平面ABCD



 平面PDC
平面PDC 平面PAD;
平面PAD;
(2)取PD中点为F,连结EF、AF,由E为PC中点,
得EF为△PDC的中位线,则EF//CD,CD=2EF.
又CD=2AB,则EF=AB.由AB//CD,则EF∥AB.
所以四边形ABEF为平行四边形,则EF//AF.
由AF 面PAD,则EF//面PAD.
面PAD,则EF//面PAD.
11.证明:(Ⅰ)连结 .
.
∵ 是
是 的中点,
的中点, 是
是 的中点,
的中点,
∴ ∥
∥ ,
,
又∵ 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面 .……………………………6分
.……………………………6分
(Ⅱ)∵
 底面
底面 ,
,
∴

 ,
,
又∵

 ,且
,且

 =
= ,
,
∴
 平面
平面 .
.
而
 平面
平面 ,
,
∴平面
 平面
平面 .………………12分
.………………12分
12.2、3
9.在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则A1到平面MBD的距离为(a).
8.正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是(线段B1C).
7.三个平面两两垂直,它们的交线交于一点O,P到三个面的距离分别为3、4、5,则OP的长为(5).
6.长方体中ABCD-A1B1C1D1中,AB=8,BC=6,在线段BD,A1C1上各有一点P、Q,在PQ上有一点M,且PM=MQ,则M点的轨迹图形的面积为 24 .
5.已知正 的边长为
的边长为 ,那么
,那么 的平面直观图
的平面直观图 的面积为
的面积为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com