10.分式:

　 ①性质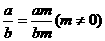　

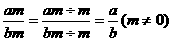
　 ②分式的值为零的条件:分子为零,同时分母不为零.

　③有意义的条件:分母不为零.

　 ④加法: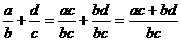

　 ⑤乘法: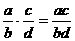

　 ⑥除法: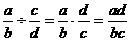

　 ⑦乘方: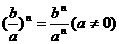

9.因式分解:将一个多项式化成n个因式乘积的形式.

方法①提取公因式地:公因式是各项的系数的最大公约数及相同字母中指数最小的.如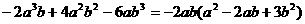

②公式法:将乘法公式反过来用.如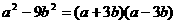

　 9m²-12mn+4n²=(3m-2n)²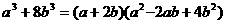　

③分组分解法:注意分组的原则是有利于因式分解.如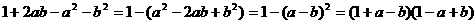

再如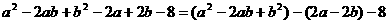

　 =

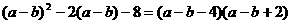
④十字相乘法:略

⑤公式法: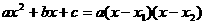,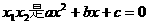的根.

　 因式分解的结果一定要使每个因式都是质式即不能再分解为止.

8.整式的加减,乘,除:

①同类项,含有字母相同,并且相同的字母的指数也相同,如.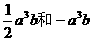

②整式的加减,将系数相加减,字母及指数不变.如.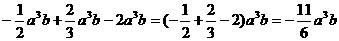

③整式乘法

(1)单项式乘单项式,如=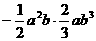

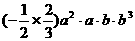
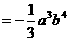
(2)多项式×单项式;利用乘法的分配律,m(a+b)=ma+mab.如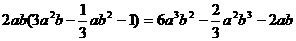

(3)多项式×多项式(m+n)(a+b)ma+mb+na+nb

④乘法公式

(1)平方差(a+b)(ab)=a²-b².此公式的特点是两项乘两项,两个括号中各有一项相同,一项互为相反,结果是相同那一项的平方减去相反那一项的平方.如:(2a+b)(-b+2a)=(2a)²-b²=4a²-b²,

　 再如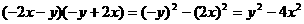

(2)完全平方公式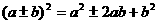结果是三项.第一项和第三项分别是括号内两项的平方式(都是正的).中间一项是两项乘积的2倍.(符号:若两项同号为正,两项异号为负)如:(m-2n)²=m²-4mn+4n².

(-m+2n)²=m²-4mn+4n², (m+2n)²=m²+4mn+4n², (-m-2n)²=m²+4mn+4n².

(3)立方和(差)公式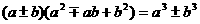

7.幂的运算法则:

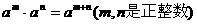
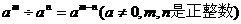
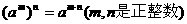
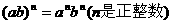
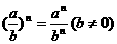
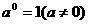
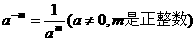
6.有理数的加减,乘,除法则

①加法:两数相加,若同号,取原来的符号,并把绝对值相加;异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,如.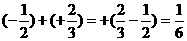

②减法:减去一个数等于加上这个数的相反数.

③乘法:两数相乘,同号得正,异号得负,并把绝对值相乘.

④除法:除以一个数等于乘以这个数的倒数.

5.绝对值:

　　 这个概念是极重要的,也是同学们很难掌握的,它的几何意义是 “在数轴上,表示一个数的点,它离开原点的距离”,具体在求一个数或一个代数式的绝对值时,应遵循“正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值仍是零”,即要化简绝对值,要分析绝对值号中的数(代数式)表示什么数,如|a-2|(a<2)因为a<2号中,绝对值号中的a-2是负数,所以|a-2|(a<2)=-(a-2)=2-a.

4.倒数:

若两个数的乘积是1,这两个数是互为例数.(注意零没有倒数)

3.数轴:

　　 规定了原点,方向和单位长度的直线,但要注意数轴上的点和有理数不是 “一一对应”,数轴上的点和实数“一一对应”,即给定一个实数,我们可以在数轴上找到表示这个实数的点,而数轴上的点表示一个实数.

2.相反数

　　 只有符号不同的两个数,如5和-5,若有一个代数式,我们表示它的相反数,只需在它的前面加“-”即可,如a的相反数是-a,a-2的相反数是-(a-2)=2-a……

1.有理数

整数和分数统称有理数.