
题目列表(包括答案和解析)
1、一次函数y=kx+b和y=bx+k在同一坐标系内的图象大致是图2-l-5中的( ) (图2-l-5)
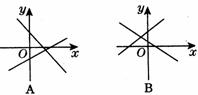
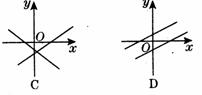
当y=360时,50x-150=360,解得x=10.2.
所以S=50×10.2+100=610.
答:需售门票 920张或 1020张,相应地需支付成本费用分别为56000元或 61000元.
点拨:正确理解题意,注意单位的统一.
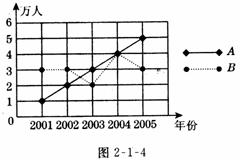 [例4](2005,重庆)如图2-1-4所示,A、B两个旅游点从2001年至2005年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:
[例4](2005,重庆)如图2-1-4所示,A、B两个旅游点从2001年至2005年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2001到2005年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人 数为4万人,为控制游客数量,A旅游点决定提高门票价格.已知门票价格x(元)与游客人数y(万人)满足函数关系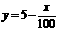 .若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
解:(1)B旅游点的旅游人数相对上一年增长最快的是2004年.
(2)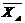 =
=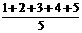 =3(万元)
=3(万元)
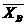 =
=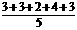 =3(万元)
=3(万元)
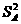 =
=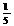 [(-2)
[(-2)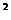 +(-1)
+(-1)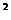 +0
+0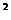 +1
+1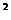 +2
+2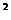 ]=2
]=2
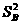 =
=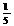 [0
[0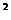 +0
+0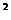 +(-1)
+(-1)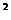 +1
+1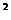 +0
+0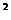 ]=
]=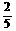
从2001至2005年,A、B两个旅游点平均每年的旅游人数均为3万人,但A旅游点较B旅游点的旅游人数波动大. (3)由题意,得5-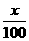 ≤4;
≤4;
解得x≥100, 100-80=20
答:A旅游点的门票至少要提高20元.
Ⅲ、综合巩固练习:(10分 90分钟)
(2)当10<x≤20时,由题意,知 50x-100=360.
所以x=9.2,S=50x+100 =50×9.2+100=560.
当10<x≤2 0时,设y=mx+n.
把点(10,350)(20,850)代入函数解析式,得

所以y=50x-150(10<x≤20),
18、(6分)解分式方程: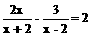 。
。
17、(6分)化简: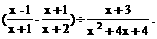
16、(6分)解不等式组: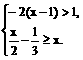
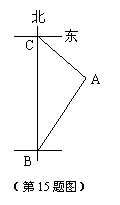
15、小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B点他
观察到仓库A在他的北偏东300处,骑行20分钟后到达C点,发现此时这座仓库正好在他的
东南方向,则这座仓库到公路的距离为________千米。
(参考数据: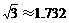 。结果保留两位有效数字。)
。结果保留两位有效数字。)
14、如右统计图显示的是绵阳某商场日用品柜台10名售货员4月份完成销
售额(单位:千元)的情况,根据统计图,我们可以计算出该柜台的人
 均销售额为_______________千元。
均销售额为_______________千元。
13、如图,AB//CD,直线l平分∠AOE,∠1=400,则∠2=________。
12、因式分解: 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com