
题目列表(包括答案和解析)
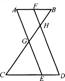
7.如图,AB//CD,AE//FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
(A)4对 (B) 5对 (C) 6对 (D)7对
6. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于(
)
若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于(
)
(A) (B)
(B)
(C)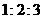 (D)
(D) 
5.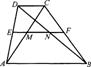
 如图,在梯形ABCD中,AB//CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( )
如图,在梯形ABCD中,AB//CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( )
(A)10cm (B)13cm(C)20cm (D)26cm
4.若0<x<1,则x,x2,x3的大小关系是( )
(A)x<x2<x3 (B)x<x3<x2 (C)x3<x2<x (D)x2<x3<x
3.已知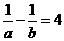 ,则
,则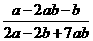 的值等于( )
的值等于( )
(A)6
(B)-6 (C)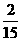 (D)
(D) 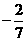
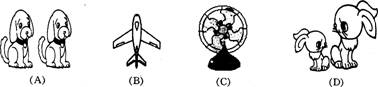
2.下列图形中,为轴对称图形的是( )
1.下列判断中正确的是( )
(A)四边相等的四边形是正方形 (B) 四角相等的四边形是正方形
(C) 对角线互相垂直的平行四边形是正方形
(D) 对角线互相垂直平分且相等的四边形是正方形
28.解(1) 抛物线
抛物线 过
过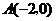 ,
,
 ·········································································································· 1分
·········································································································· 1分
 点
点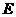 在抛物线上,
在抛物线上,
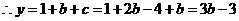 ,
,
 点
点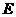 的坐标为
的坐标为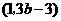 .·················································································· 3分
.·················································································· 3分
(2)由(1)得 ,
,
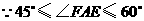 ,
,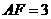 ,
,
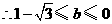 .······························································································· 6分
.······························································································· 6分
(3) 的面积有最大值,············································································ 7分
的面积有最大值,············································································ 7分
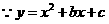 的对称轴为
的对称轴为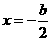 ,
,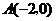 ,
,
 点
点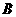 的坐标为
的坐标为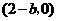 ,··················································································· 8分
,··················································································· 8分
由(1)得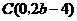 ,
,
而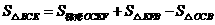
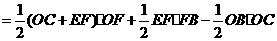
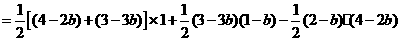
 ,······························································································ 10分
,······························································································ 10分
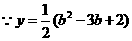 的对称轴是
的对称轴是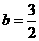 ,
,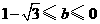
 当
当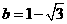 时,
时,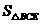 取最大值,
取最大值,
其最大值为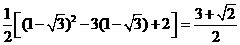 . 12分
. 12分
25.解:(1)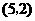 ,
, ,
,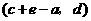 .····················································· 2分
.····················································· 2分
(2)分别过点 作
作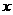 轴的垂线,垂足分别为
轴的垂线,垂足分别为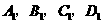 ,
,
 分别过
分别过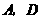 作
作 于
于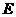 ,
,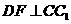 于点
于点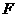 .
.
在平行四边形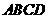 中,
中, ,又
,又 ,
,
 .
.
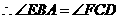 .
.
又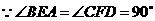 ,
,
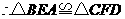 .·································································································· 5分
.·································································································· 5分
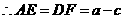 ,
,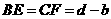 .
.
设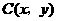 .由
.由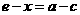 ,得
,得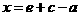 .
.
由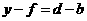 ,得
,得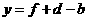 .
.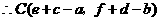 .································ 7分
.································ 7分
(此问解法多种,可参照评分)
(3) ,
,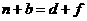 或
或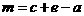 ,
,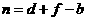 .························· 9分
.························· 9分
(4)若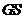 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得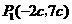 .要使
.要使 在抛物线上,
在抛物线上,
则有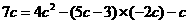 ,即
,即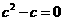 .
.
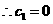 (舍去),
(舍去),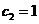 .此时
.此时 .································································ 10分
.································································ 10分
若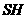 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得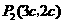 ,同理可得
,同理可得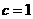 ,此时
,此时 .
.
若 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得 ,同理可得
,同理可得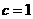 ,此时
,此时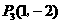 .
.
综上所述,当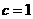 时,抛物线上存在点
时,抛物线上存在点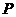 ,使得以
,使得以 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
符合条件的点有 ,
, ,
,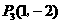 . 12分
. 12分
乐山市2007年 28.如图(16),抛物线
28.如图(16),抛物线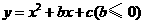 的图象与
的图象与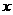 轴交于
轴交于 两点,与
两点,与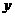 轴交于点
轴交于点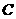 ,其中点
,其中点 的坐标为
的坐标为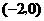 ;直线
;直线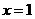 与抛物线交于点
与抛物线交于点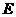 ,与
,与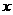 轴交于点
轴交于点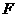 ,且
,且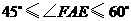 .
.
(1)用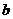 表示点
表示点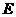 的坐标;
的坐标;
(2)求实数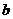 的取值范围;
的取值范围;
(3)请问 的面积是否有最大值?
的面积是否有最大值?
若有,求出这个最大值;若没有,请说明理由.
(1) .··································································································· 2分
.··································································································· 2分
(2)点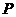 的运动速度为2个单位/秒.·········································································· 4分
的运动速度为2个单位/秒.·········································································· 4分
(3)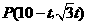 (
( )
)
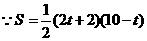 ································································································ 6分
································································································ 6分
 .
.
 当
当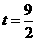 时,
时,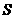 有最大值为
有最大值为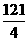 ,
,
此时 .····································································································· 9分
.····································································································· 9分
(4)当点 沿这两边运动时,
沿这两边运动时,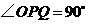 的点
的点 有2个.····································· 11分
有2个.····································· 11分
①当点 与点
与点 重合时,
重合时,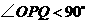 ,
,
当点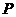 运动到与点
运动到与点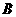 重合时,
重合时, 的长是12单位长度,
的长是12单位长度,
作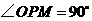 交
交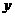 轴于点
轴于点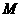 ,作
,作 轴于点
轴于点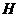 ,
,
由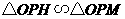 得:
得: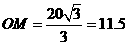 ,
,
所以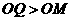 ,从而
,从而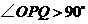 .
.
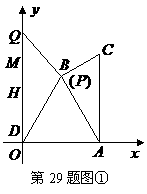 所以当点
所以当点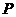 在
在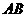 边上运动时,
边上运动时,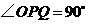 的点
的点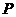 有1个.··································· 13分
有1个.··································· 13分
②同理当点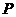 在
在 边上运动时,可算得
边上运动时,可算得 .
.
而构成直角时交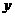 轴于
轴于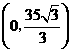 ,
,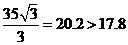 ,
,
所以 ,从而
,从而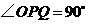 的点
的点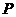 也有1个.
也有1个.
所以当点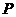 沿这两边运动时,
沿这两边运动时,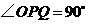 的点
的点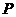 有2个.······································· 14分
有2个.······································· 14分
无锡市2007年28.(本小题满分10分)
如图,平面上一点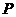 从点
从点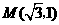 出发,沿射线
出发,沿射线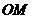 方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以
方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以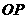 为对角线的矩形
为对角线的矩形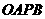 的边长
的边长 ;过点
;过点 且垂直于射线
且垂直于射线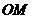 的直线
的直线 与点
与点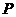 同时出发,且与点
同时出发,且与点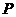 沿相同的方向、以相同的速度运动.
沿相同的方向、以相同的速度运动.
(1)在点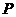 运动过程中,试判断
运动过程中,试判断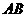 与
与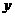 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
(2)设点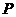 与直线
与直线 都运动了
都运动了 秒,求此时的矩形
秒,求此时的矩形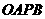 与直线
与直线 在运动过程中所扫过的区域的重叠部分的面积
在运动过程中所扫过的区域的重叠部分的面积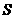 (用含
(用含 的代数式表示).
的代数式表示).


解:(1) 轴.···························· 1分
轴.···························· 1分
理由:
 中,
中,
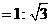 ,
, .····· 2分
.····· 2分
设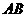 交
交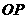 于点
于点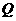 ,交
,交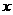 轴于点
轴于点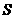 ,
, 矩形的对角线互相平分且相等,则
矩形的对角线互相平分且相等,则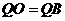 ,
,
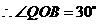 ,过点
,过点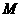 作
作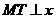 轴于
轴于 ,则
,则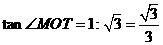 ,
,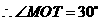 ,
,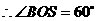 ,
,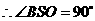 ,
,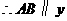 轴.······················· 3分
轴.······················· 3分
(2)设 在运动过程中与射线
在运动过程中与射线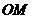 交于点
交于点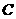 ,过点
,过点 且垂直于射线
且垂直于射线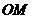 的直线交
的直线交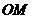 于点
于点 ,过点
,过点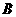 且垂直于射线
且垂直于射线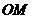 的直线交
的直线交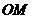 于点
于点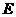 ,则
,则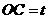 .
.
 ,
,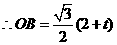 ,
,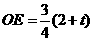 ,
,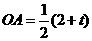 ,
, .
.
······································ 4分
①当 ,即
,即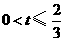 时,
时,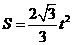 .·············· 6分
.·············· 6分
②当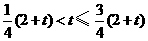 ,即
,即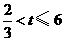 时,设直线
时,设直线 交
交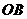 于
于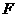 ,交
,交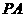 于
于 ,则
,则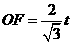 ,
,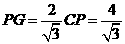 ,
,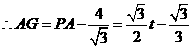 ,
,
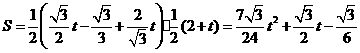 .··········· 8分
.··········· 8分
③当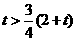 ,即
,即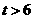 时,
时, ,
,
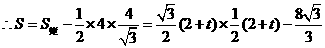
 ………………………………………………10分
………………………………………………10分
扬州市2007年26.(本题满分14分)
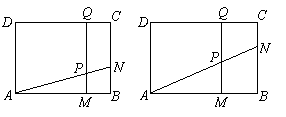
如图,矩形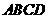 中,
中,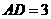 厘米,
厘米,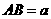 厘米(
厘米(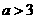 ).动点
).动点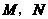 同时从
同时从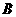 点出发,分别沿
点出发,分别沿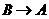 ,
,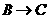 运动,速度是
运动,速度是 厘米/秒.过
厘米/秒.过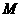 作直线垂直于
作直线垂直于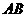 ,分别交
,分别交 ,
,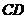 于
于 .当点
.当点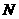 到达终点
到达终点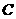 时,点
时,点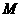 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为 秒.
秒.
(1)若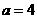 厘米,
厘米,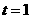 秒,则
秒,则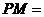 ______厘米;
______厘米;
(2)若 厘米,求时间
厘米,求时间 ,使
,使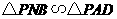 ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形 与梯形
与梯形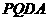 的面积相等,求
的面积相等,求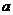 的取值范围;
的取值范围;
 (4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形 ,梯形
,梯形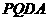 ,梯形
,梯形 的面积都相等?若存在,求
的面积都相等?若存在,求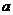 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
26.(1)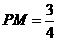 ,
,
(2)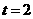 ,使
,使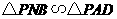 ,相似比为
,相似比为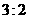
(3)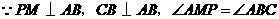 ,
,
 ,
,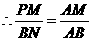 即
即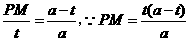 ,
,
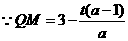
当梯形 与梯形
与梯形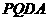 的面积相等,即
的面积相等,即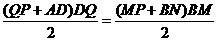
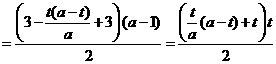 化简得
化简得 ,
,
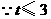 ,
,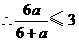 ,则
,则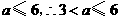 ,
,
(4) 时,梯形
时,梯形 与梯形
与梯形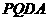 的面积相等
的面积相等
 梯形
梯形 的面积与梯形
的面积与梯形 的面积相等即可,则
的面积相等即可,则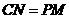
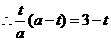 ,把
,把 代入,解之得
代入,解之得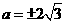 ,所以
,所以 .
.
所以,存在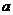 ,当
,当 时梯形
时梯形 与梯形
与梯形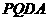 的面积、梯形
的面积、梯形 的面积相等.
的面积相等.
江西省南昌市2007年25.实验与探究
(1)在图1,2,3中,给出平行四边形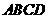 的顶点
的顶点 的坐标(如图所示),写出图1,2,3中的顶点
的坐标(如图所示),写出图1,2,3中的顶点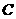 的坐标,它们分别是 , ,
;
的坐标,它们分别是 , ,
;
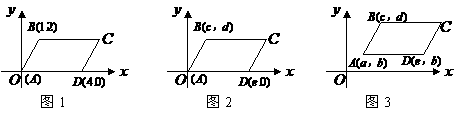

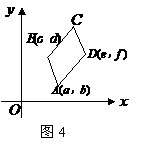
(2)在图4中,给出平行四边形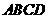 的顶点
的顶点 的坐标(如图所示),求出顶点
的坐标(如图所示),求出顶点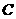 的坐标(
的坐标(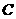 点坐标用含
点坐标用含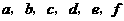 的代数式表示);
的代数式表示);

归纳与发现
(3)通过对图1,2,3,4的观察和顶点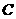 的坐标的探究,你会发现:无论平行四边形
的坐标的探究,你会发现:无论平行四边形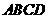 处于直角坐标系中哪个位置,当其顶点坐标为
处于直角坐标系中哪个位置,当其顶点坐标为 (如图4)时,则四个顶点的横坐标
(如图4)时,则四个顶点的横坐标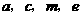 之间的等量关系为
;纵坐标
之间的等量关系为
;纵坐标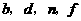 之间的等量关系为
(不必证明);
之间的等量关系为
(不必证明);
运用与推广
(4)在同一直角坐标系中有抛物线 和三个点
和三个点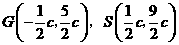 ,
,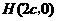 (其中
(其中 ).问当
).问当 为何值时,该抛物线上存在点
为何值时,该抛物线上存在点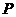 ,使得以
,使得以 为顶点的四边形是平行四边形?并求出所有符合条件的
为顶点的四边形是平行四边形?并求出所有符合条件的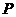 点坐标.
点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com