(一)比例的性质

　　 1.比例的基本性质: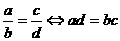

此性质非常重要,要求掌握把比例式化成等积式、把等积式转化成比例的方法.

2.合、分比性质: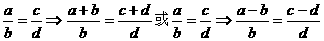

注意:此性质是分子加(减)分母比分母,不变的是分母.

如:已知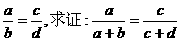

证明:∵　 ∴　 ∴　 ∴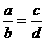

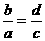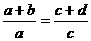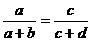
3.等比性质:若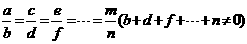则.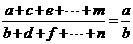

4.比例中项:若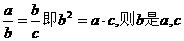的比例中项.

3.由题意得

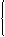　 P点坐标是 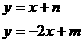的解，即P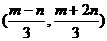

　 ∵AB=2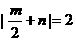　 　　

　 ∴　

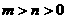
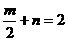
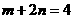
　　 SΔABP=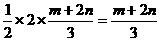

　　 SΔAOQ=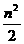

　 ∴　　

　 ∴　

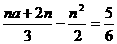
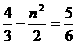
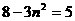
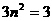
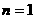
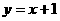
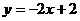
2.(1)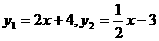

(2)由题意得B(-2,0),A(0,4),D(6,0),C(0,-3)

　 S_四边形ABCD=SΔABC+SΔADC

　 ∵A(0,4)　 C(0,-3)

　 ∴AC=7

　　 SΔABC=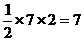

　　 SΔADC=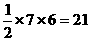

　 ∴S_四边形ABCD=28

(3)由题意得E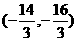　　　 SΔAEC=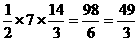

　 SΔAEC=SΔAEC-SΔABC=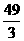-7=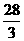

　 ∴SΔBEC:S_四边形ABCD=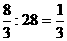

1.A　　 2.B　　 3.B　　 4.B　　 5.C

(3)1.由题意得C(3,-1) A(4,0) 设B()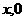

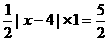
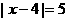
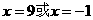
即B点坐标是(0,9)或(-1,0)

用(9,0)和(3,-1)两点求解析式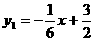

用(-1,0)和(3,-1)两点求解析式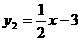

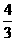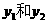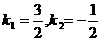7.　 解题指导:将(2,-1)代入解得:,所以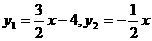.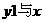轴交于A(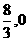),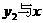轴交于B(0,0).所以AB=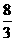,高是|-1|=1,所以SΔ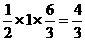

(2)选择题:

6.SΔABC=25,SΔPCQ=.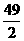

　 解题指导:由题意得C(7,10),A(2,0),B(-3,0),P(0,-4),Q(0,3),则AB=|2-(-3)|=5,高是C的纵坐标10.所以SΔABC=.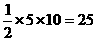

5.

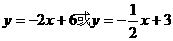
3. 　3,-1或4

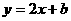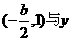　 解题指导:直线与轴交于轴交于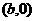由题意,,解得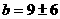

(1)1.　 -5, 一、三、四象限, 增大

2． 二、三、四象限,(-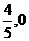),(0,-4),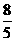

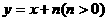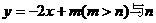3.如图,已知直线PA,与轴交于A,与轴交于Q,另一条直线轴交于B,而直线交于P

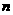求: (1)A,B,Q,P四点的坐标(用或表示)

　　 (2)若AB=2,且S_四边形PQOB=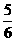,求两个函数的解析式.

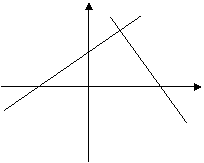　　　　　 　　　　　　　　　　　　y

　　　　　　　　　　　　　　　　　　　 P

　　　　　　　　　　　　　　　 Q

　　　　　　　　　　　　　 A　　 0　　　　　 B　 x