
题目列表(包括答案和解析)
7.正余弦值的取值范围 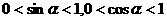
6.同角间的三角函数恒等式
①平方关系 
②倒数关系 
③比的关系 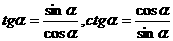
在这四个关系中,①②用的最多.
5.四个三角函数性质
当∠A从30°增长到45°,再增长到60°,它的正弦值从 增到
增到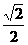 ,再增到
,再增到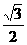 .说明正弦值随着∠A的增大而增大.即两个锐角,大角的正弦大,反之两个锐角的正弦值比较,正弦值越大,角越大.如
.说明正弦值随着∠A的增大而增大.即两个锐角,大角的正弦大,反之两个锐角的正弦值比较,正弦值越大,角越大.如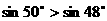 .
.
同理正切函数也具有相同的性质,如tg53°>tg40°,再比如比较tg40°和ctg40°的大小,将ctg40°化成tg50°.∵tg40°<tg50°,∴tg40°<ctg40°.已知 ,则一定有
,则一定有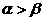 的结论.再如
的结论.再如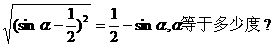
解: 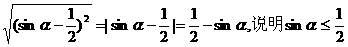
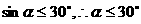
而余弦,余切则是函数值随着角度的增大而减小,即角越大,余弦(切)值越小,反之余弦(切)值越大,它的角越小.
如cos40°>cos50° ctg20°>ctg50°
若
比较两个函数值的大小,通常化成同名函数,再根据性质比较大小.
例1:已知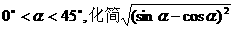
解:

比如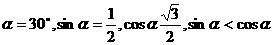 .
.
再如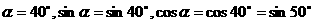

所以
例2:已知
解:
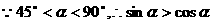
(在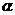 的取值范围内任取2个角验证即可)
的取值范围内任取2个角验证即可)
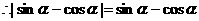
例3.如已知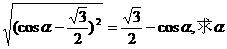 的取值范围.
的取值范围.
解: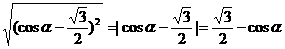
说明

上述四个函数的性质掌握起来较难,要想法弄懂,多思,多练.
4.互为余角的函数关系式:
90°-∠A与∠A是互为余角.
有



通过这四个关系式,可以将正,余弦互化,正切与余切互化.
如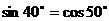


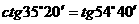
2.三角函数定义:
 我们规定
我们规定
①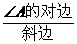 叫∠A的正弦.记作
叫∠A的正弦.记作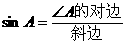
② 叫∠A的余弦.记作
叫∠A的余弦.记作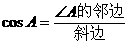
③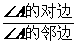 叫∠A的正切.记作
叫∠A的正切.记作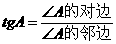
④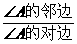 叫∠A的余切.记作
叫∠A的余切.记作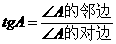
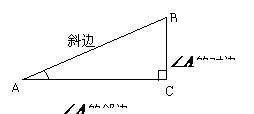
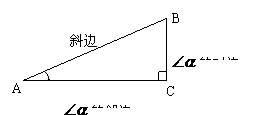
这四个三角函数定义是人们规定的,不能问为什么这样规定?这四个函数定义是本章重点中的重点,要达到①在直角三角形中,给我们一个锐角,我们知道这个角的正弦,余弦,正切,余切是哪两条线段的比.反之②在直角三角形中给我们两条线段的比,我们知道是哪个锐角的什么函数.
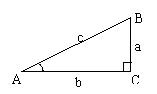 如图
如图
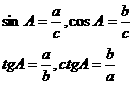
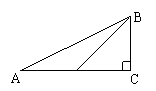
|
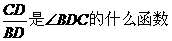
因为CD是∠BDC的邻边,BD是斜边,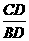 是∠BDC的邻边比斜边,所以
是∠BDC的邻边比斜边,所以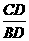 是∠BDC的余弦.
是∠BDC的余弦.
 3.特殊角的三角函数值
3.特殊角的三角函数值
①∠A=30°
此时,设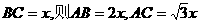
则



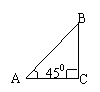
②∠A=45°
此时,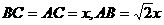
则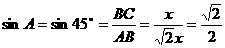
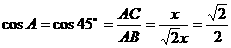


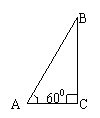
③∠A=60°
此时设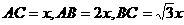
则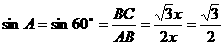

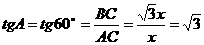
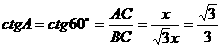
|
角度 函数值 |
30° |
45° |
60° |
 |
 |
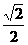 |
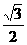 |
 |
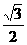 |
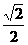 |
 |
 |
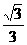 |
1 |
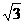 |
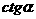 |
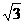 |
1 |
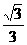 |
1.锐角三角函数是关于直角三角形两直角边及斜边和直角三角形的一个锐角间的关系,设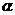 是直角三角形的一个锐角
是直角三角形的一个锐角
则围绕三边有六个比值,即① ;②
;②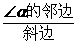 ;③
;③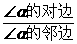 ;④
;④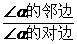 ;⑤
;⑤ ;⑥
;⑥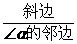 .而①②③④这四个线段的比就是初三所学习的正弦、斜弦、正切、余切函数,这四个函数是角
.而①②③④这四个线段的比就是初三所学习的正弦、斜弦、正切、余切函数,这四个函数是角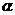 的变化而变化,而与边长无关.如,设
的变化而变化,而与边长无关.如,设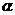 =30°,无论它的对边和斜边多长
=30°,无论它的对边和斜边多长 .
.
(四)①由

 得
得
②∵ ∴
∴ 与
与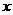 轴交于A(0,0)和B(3,0)
轴交于A(0,0)和B(3,0)
设存在
由题意得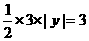


将 舍去(若
舍去(若 点必在
点必在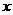 轴上方,此时△AB
轴上方,此时△AB 是钝角三角形,与△A
是钝角三角形,与△A B是锐角三角形不符)
B是锐角三角形不符)
当 时,
时, 
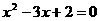
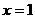

∴
 也会在[因为
也会在[因为 ]在对称轴左边.
]在对称轴左边.
∴适合条件的点 是(2,-2)
是(2,-2)
 y
y 
A B

(三)1.D 2.C 3.C
(二)1. 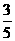 2.
2. 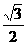 3.
3. 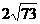 4. 30° 5.
4. 30° 5. 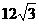 6. (9,0),(0,-3)
6. (9,0),(0,-3) 
7. 2; 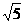 8.
8.  9. ¨5或3 10. (3,-2) 11.
9. ¨5或3 10. (3,-2) 11. 
12.
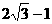 13. 4 14.
13. 4 14.  15.
15.
16. 提示:设
提示:设 轴交于(0,2)
y
轴交于(0,2)
y
它与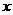 轴交于(
轴交于(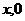 ),则S△AOB=
),则S△AOB= A(0,2)
A(0,2)


∴与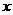 轴交于(7,0)和(-7,0) 0 B(
轴交于(7,0)和(-7,0) 0 B(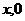 ) x
) x
将 代入公式
代入公式 ,
,
将 代入得
代入得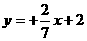
17.
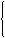 交点C的坐标是
交点C的坐标是  的解
的解  S△ABC=25 S△CPQ=
S△ABC=25 S△CPQ=
18.提示: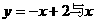 轴交于(2,0),
轴交于(2,0), 与
与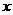 轴交于(
轴交于(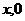 )
)
则

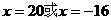
∴B(20,0)或(-16,0)分别和C(3,-1)代入 得
得
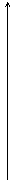 ∴
∴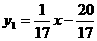 和
和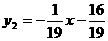 y
y


0 A(2,0) B(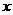 ,0)
,0)
C(3,-1)
19.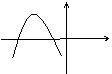 二次函数
二次函数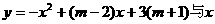 轴交于A(
轴交于A(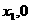 )和B(
)和B( ),
), 是
是 的根.线段OA的长是
的根.线段OA的长是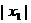 ,线段OB的长是
,线段OB的长是 ,由题意得:
,由题意得: ,若图象是
,若图象是
A(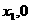 ) B(
) B( )
)
则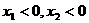

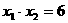 两根之积是6
两根之积是6


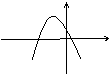 若图象是
若图象是
A(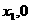 ) B(
) B( )
)
则
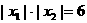



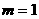
∴ S△ABC=3或15
S△ABC=3或15
(一)1.√ 2.√ 3.× 4.× 5.× 6.√
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com