
题目列表(包括答案和解析)
6.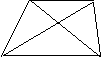 在梯形ABCD中AD∥BC,且AD=2,
A D
在梯形ABCD中AD∥BC,且AD=2,
A D
BC=4,AC=3,BD=3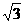 ,则∠DBC等于:
,则∠DBC等于:
A.30° B.45° C.60° D.75° B C
5.三角形三条边长为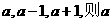 的取值范围是:
的取值范围是:
A.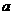 >4
B.
>4
B.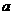 >3
C.
>3
C.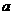 >2
D.
>2
D.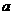 >1
>1
4.在Rt△ABC中,∠ACB=90°,CE⊥AB, C
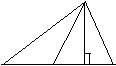 CD是中线,∠B=60°,AC=
CD是中线,∠B=60°,AC=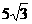 ,
,
则DE等于:
A.2 B.2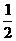 C.
C.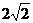 D.
D.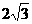 A D E B
A D E B
3.顺次连结梯形四边中点所得四边形是:
A.平行四边形 B.菱形 C.矩形 D.正方形
2.两个相似三角形中线的比是1:3,则它们的面积比是:
A.1: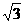 B.1:3 C.
B.1:3 C.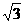 :3
D.1:9
:3
D.1:9
1.已知直角三角形中30°角所对的直角边长是3cm,则斜边的长是:
A.3cm B.6cm C.8cm D.10cm
28.(本题满分12分)
已知:如图,在直角梯形ABCD中,AD∥BC,BC=5cm,CD=6cm,∠DCB=60°,∠ABC=90°.等边三角形MPN(N为不动点)的边长为acm,边MN和直角梯形ABCD的底边BC都在直线l上,NC=8cm,将直角梯形ABCD向左翻折180°,翻折一次得图形①,翻折二次得图形②,如此翻折下去.
(1)将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长a≥2cm,那么这时两图形重叠部分的面积是多少?
(2)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD的面积,那么这时等边三角形的边长a至少应为多少?
 (3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD面积的一半,那么这时等边三角形的边长至少应为多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分面积等于直角梯形ABCD面积的一半,那么这时等边三角形的边长至少应为多少?
27.(本题满分12分)
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取弧AB上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
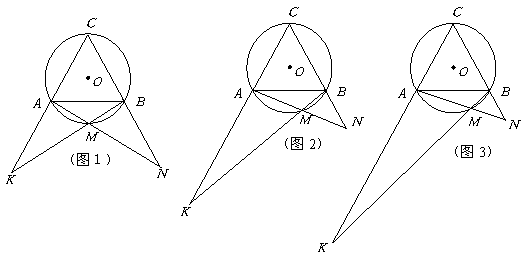 (1)如图1、图2、图3,M分别为弧AB的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK·BN的值(精确到0.01)并将结果填入下表中:
(1)如图1、图2、图3,M分别为弧AB的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK·BN的值(精确到0.01)并将结果填入下表中:
|
|
△ABC的边长 |
AK·BN的值 |
|
图1 |
2 |
|
|
图2 |
2 |
|
|
图3 |
2 |
|
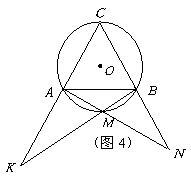
(2)如图4,当M为弧AB上任意一点时,根据(1)的结果,猜想AK·BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
26.(本题满分10分)
两人同去某风景区游玩, 每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度, 也不知道汽车开过来的顺序. 两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车. 而乙则是先观察后上车, 当第一辆车开来时, 他不上车, 而是仔细观察车的舒适状况, 如果第二辆车的舒适程度比第一辆好, 他就上第二辆车; 如果第二辆车不比第一辆好, 他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等, 请尝试着解决下面的问题:
(1) 三辆车按出现的先后顺序工有哪几种不同的可能?
(2) 你认为甲、乙采用的方案, 哪一种方案使自己乘上等车的可能性大? 为什么?
25.(本题满分10分)
 周日,刚学过解直角三角形的小岩打算去测量河对岸的烟囱高度,他先向老师借了两块木制大三角板,站在地上的C点,测得顶点A的仰角是30°,接着又向前走20米到达D地(C,D,B在同一条直线上),测得顶点A的仰角是45°,又知测量时三角板平行于地面的一边到地面的距离始终为1.2米(如图),于是他就计算出了烟囱的高度,你能把小明的计算过程与结果写出来吗?(结果可保留根号)
周日,刚学过解直角三角形的小岩打算去测量河对岸的烟囱高度,他先向老师借了两块木制大三角板,站在地上的C点,测得顶点A的仰角是30°,接着又向前走20米到达D地(C,D,B在同一条直线上),测得顶点A的仰角是45°,又知测量时三角板平行于地面的一边到地面的距离始终为1.2米(如图),于是他就计算出了烟囱的高度,你能把小明的计算过程与结果写出来吗?(结果可保留根号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com