
题目列表(包括答案和解析)
13、(2007福建晋江)如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了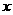 秒。
秒。
⑴请直接写出PN的长;(用含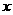 的代数式表示)
的代数式表示)
⑵若0秒≤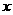 ≤1秒,试求△MPA的面积S与时间
≤1秒,试求△MPA的面积S与时间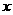 秒的函数关系式,利用函数图象,求S的最大值。
秒的函数关系式,利用函数图象,求S的最大值。
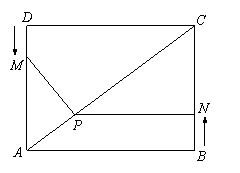 ⑶若0秒≤
⑶若0秒≤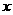 ≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有
≤3秒,△MPA能否为一个等腰三角形?若能,试求出所有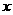 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
解:⑴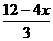 ;
;
⑵延长NP交AD于点Q,则PQ⊥AD,由⑴得:PN=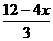 ,
,
则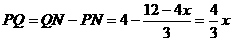 。
。
依题意,可得: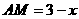
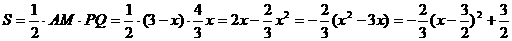
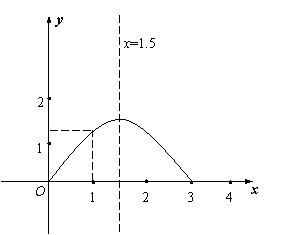 ∵0≤
∵0≤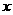 ≤1.5
≤1.5
即函数图象在对称轴的左侧,函数值S
随着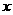 的增大而增大。
的增大而增大。
∴当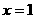 时,S有最大值 ,S最大值=
时,S有最大值 ,S最大值=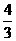 。
。
⑶△MPA能成为等腰三角形,
共有三种情况,以下分类说明:
①若PM=PA,
∵PQ⊥MA ∴MQ=QA=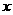
又DM+MQ+QA=AD ∴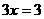 ,即
,即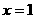
②若MP=MA,则MQ=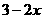 ,PQ=
,PQ=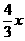 ,MP=MA=
,MP=MA=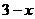
在Rt△PMQ中,由勾股定理得: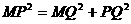
∴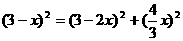 ,解得:
,解得: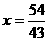 (
(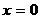 不合题意,舍去)
不合题意,舍去)
③若AP=AM,
由题意可得: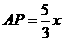 ,AM=
,AM=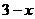
∴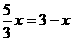 ,解得:
,解得: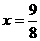
综上所述,当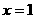 ,或
,或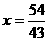 ,或
,或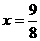 时,△MPA是等腰三角形。
时,△MPA是等腰三角形。
12、(2007福建福州)为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的图弧构成的图案,既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出三种不同的的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种.

解:以下为不同情形下的部分正确画法,答案不唯一.(满分8分)

11、(2007南充)如图, 等腰梯形ABCD中,AB=15,AD=20,∠C=30º.点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.
(1)设ND的长为x,用x表示出点N到AB的距离,并写出x的取值范围.
(2)当五边形BCDNM面积最小时,请判断△AMN的形状.


解:(1)过点N作BA的垂线NP,交BA的延长线于点P. ………………(1分)
由已知,AM=x,AN=20-x.
∵ 四边形ABCD是等腰梯形,AB∥CD,∠D=∠C=30º,
∴ ∠PAN=∠D=30º.
在Rt△APN中,PN=ANsin∠PAN=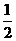 (20-x),
即点N到AB的距离为
(20-x),
即点N到AB的距离为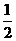 (20-x). ………………………………(3分)
∵ 点N在AD上,0≤x≤20,点M在AB上,0≤x≤15,
∴ x的取值范围是 0≤x≤15. ………………………………(4分)
(2)根据(1),S△AMN=
(20-x). ………………………………(3分)
∵ 点N在AD上,0≤x≤20,点M在AB上,0≤x≤15,
∴ x的取值范围是 0≤x≤15. ………………………………(4分)
(2)根据(1),S△AMN=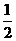 AM•NP=
AM•NP=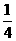 x(20-x)=
x(20-x)=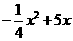 . ……(5分)
∵
. ……(5分)
∵ 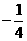 <0,∴ 当x=10时,S△AMN有最大值. …………………………(6分)
又∵ S五边形BCDNM=S梯形-S△AMN,且S梯形为定值,
∴ 当x=10时,S五边形BCDNM有最小值. …………………………(7分)
当x=10时,即ND=AM=10,AN=AD-ND=10,即AM=AN.
则当五边形BCDNM面积最小时,△AMN为等腰三角形. …………(8分)
<0,∴ 当x=10时,S△AMN有最大值. …………………………(6分)
又∵ S五边形BCDNM=S梯形-S△AMN,且S梯形为定值,
∴ 当x=10时,S五边形BCDNM有最小值. …………………………(7分)
当x=10时,即ND=AM=10,AN=AD-ND=10,即AM=AN.
则当五边形BCDNM面积最小时,△AMN为等腰三角形. …………(8分)


10、(2007四川资阳)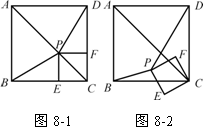 如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1) 求证:BP=DP;
(2) 如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .
⑴ 解法一:在△ABP与△ADP中,利用全等可得BP=DP.
解法二:利用正方形的轴对称性,可得BP=DP.
⑵ 不是总成立 .当四边形PECF绕点C按逆时针方向旋转,点P旋转到BC边上时,DP >DC>BP,此时BP=DP不成立.
说明:未用举反例的方法说理的不得分.
⑶ 连接BE、DF,则BE与DF始终相等.
在图8-1中,可证四边形PECF为正方形,
在△BEC与△DFC中,可证△BEC≌△DFC .
从而有 BE=DF
9、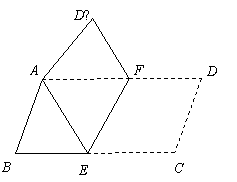 (2007山东青岛)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
(2007山东青岛)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.………2′
∴∠B=∠D′,AB=AD′,
∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.
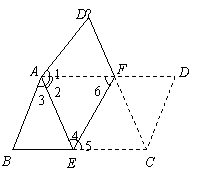 ∴∠1=∠3.
∴∠1=∠3.
∴△ABE ≌△A D′F. ……………4′
⑵ 四边形AECF是菱形.
由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠5=∠6.∴∠4=∠6.∴AF=AE.
∵AE=EC, ∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
∵AF=AE,
∴四边形AECF是菱形.
8、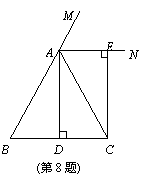 (2007淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(2007淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形
ADCE是一个正方形?并给出证明.
(1)证明:在△A BC中, AB=AC,AD⊥BC.
∴ ∠BAD=∠DAC. ………………………………1分
∵ AN是△ABC外角∠CAM的平分线,
∴ 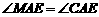 .…………………………………………2分
.…………………………………………2分
∴ ∠DAE=∠DAC+∠CAE=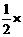 180°=90°.……………3分
180°=90°.……………3分
又 ∵ AD⊥BC,CE⊥AN,
∴ 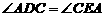 =90°, ………………………………4分
=90°, ………………………………4分
∴ 四边形ADCE为矩形. ………………………………5分
(2)说明:给出正确条件得1分,证明正确得2分.
例如,当AD=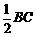 时,四边形ADCE是正方形.…………6分
时,四边形ADCE是正方形.…………6分
证明:∵ AB=AC,AD⊥BC于D.
∴ DC=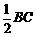 . ………………………………………7分
. ………………………………………7分
又 AD=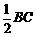 ,∴ DC=AD.
,∴ DC=AD.
由(1)四边形ADCE为矩形,
∴ 矩形ADCE是正方形.
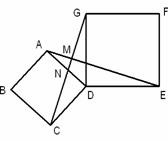
7、(2007甘肃陇南)四边形ABCD、DEFG都是正方形,连接AE、CG.
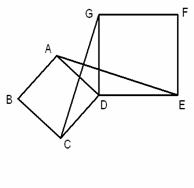 (1)求证:AE=CG;
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,
并证明你的猜想.
(1) 证明: 如图,
∵ AD=CD,DE=DG,∠ADC=∠GDE=90o,
 又 ∠CDG=90o
+∠ADG=∠ADE,
又 ∠CDG=90o
+∠ADG=∠ADE,
∴ △ADE≌△CDG. ∴ AE=CG.
(2)猜想: AE⊥CG.
证明: 如图,
设AE与CG交点为M,AD与CG交点为N.
∵ △ADE≌△CDG, ∴ ∠DAE=∠DCG.
又∵ ∠ANM=∠CND, ∴ △AMN∽△CDN.
∴ ∠AMN=∠ADC=90o.∴ AE⊥CG.
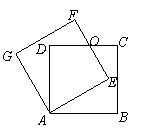
6、(2007江苏扬州)如图,正方形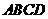 绕点
绕点 逆时针旋转
逆时针旋转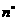 后得到正方形
后得到正方形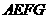 ,边
,边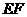 与
与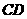 交于点
交于点 .
.
(1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为 ,重叠部分(四边形
,重叠部分(四边形 )的面积为
)的面积为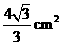 ,求旋转的角度
,求旋转的角度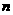 .
.
 解:(1)我连结的两条相交且互相垂直的线段是______和______.
解:(1)我连结的两条相交且互相垂直的线段是______和______.
理由如下:
(2)
(1)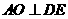
证明: 在
在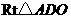 与
与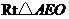 中,
中,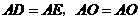 ,
,
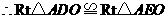 ,
,
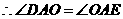 (即
(即 平分
平分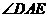 )
)
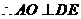 (等腰三角形的三线合一)
(等腰三角形的三线合一)
注:其它的结论也成立如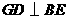 .
.
(2)
 四边形
四边形 的面积为
的面积为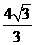 ,
,
 三角形
三角形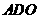 的面积
的面积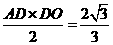 ,
,
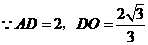 ,
,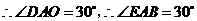 .
.
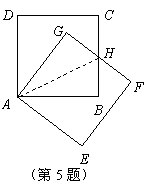
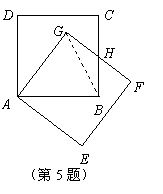
5、(2007浙江台州)把正方形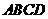 绕着点
绕着点 ,按顺时针方向旋转得到正方形
,按顺时针方向旋转得到正方形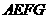 ,边
,边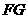 与
与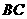 交于点
交于点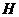 (如图).试问线段
(如图).试问线段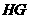 与线段
与线段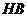 相等吗?
相等吗?
请先观察猜想,然后再证明你的猜想.
 解:
解: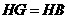 .
.
证法1:连结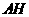 ,
,
 四边形
四边形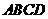 ,
,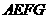 都是正方形.
都是正方形.

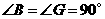 .
.
由题意知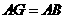 ,又
,又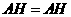 .
.
 ,
,
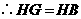 .
.
证法2:连结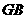 .
.
 四边形
四边形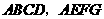 都是正方形,
都是正方形,
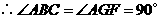 .
.
由题意知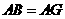 .
.
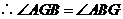 .
.
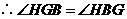 .
.
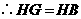 .
.
4、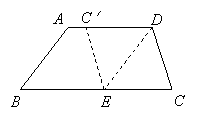 (2007云南双柏)如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
(2007云南双柏)如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.
证明:根据题意可知 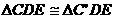
则 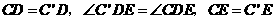
∵AD//BC ∴∠C′DE=∠CED
∴∠CDE=∠CED ∴CD=CE
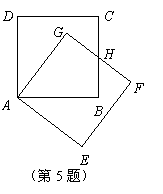 ∴CD=C′D=C′E=CE ∴四边形CDC′E为菱形
∴CD=C′D=C′E=CE ∴四边形CDC′E为菱形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com