
题目列表(包括答案和解析)
3、垂线的性质
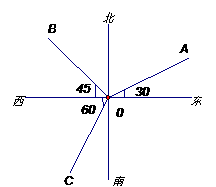 (1)过一点有且只有 条直线与已知直线垂直。
(1)过一点有且只有 条直线与已知直线垂直。
(2)直线外一点到直线上的点的距离中, 线段最短。
2、相交线与平行线
(1)同一平面内两条直线的位置关系: 、 。
 点到直线的距离:直线外一点到这条直线的
的长度。
点到直线的距离:直线外一点到这条直线的
的长度。
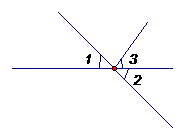
(2)对顶角的性质:对顶角 。
如右图, 与 是对顶角
(3)过直线外一点,有且仅有 条直线与这条直线平行。
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相 。
即a∥b, a∥c,则
(4) 平行线的性质(特征)
两直线 ,同位角 。
两直线 ,内错角 。
两直线 ,同旁内角 。
(5)平行线的判定(识别)
同位角 ,两直线 。
内错角 ,两直线 。
同旁内角 ,两直线 。
1、 线段与角
线段与角
(1)右图,线段有
直线有
射线有 (写两条)
(2)直线公理:经过 点有且仅有一条直线。
(3)线段公理:两点之间 最短。
(4)余角:∠1和∠2互余,则∠1+∠2=
余角的性质: 角或 角的余角相等。
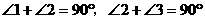 ,则
=
,则
=
(5)补角:∠1和∠2互补,则∠1+∠2=
补角的性质: 角或 角的补角相等。
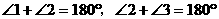 ,则
=
,则
=
(6)直角等于 度,平角等于 度,周角等于 度。
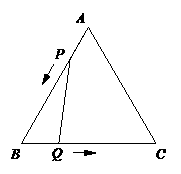
12、(2007甘肃白银等)如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.
在图(1)中,
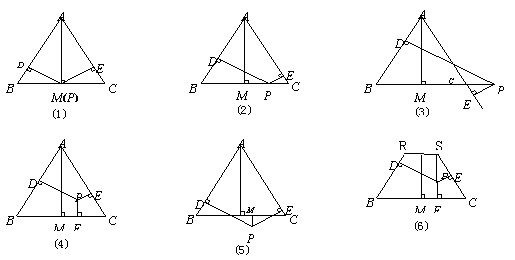
点P是边BC的中点,此时h3=0,可得结论: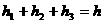 .
.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中, h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4) (附加题2分)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60o, RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为: ;图(4)与图(6)中的等式有何关系?
解:(1)图②-⑤ 中的关系依次是:
h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h; h1+h2-h3=h.
(2)图②中,h1+h2+h3=h.
证法一: ∵ h1=BPsin60o,h2=PCsin60o,h3=0,
∴ h1+h2+h3=BPsin60o+PCsin60o
=BCsin60o=ACsin60o=h.
证法二:连结AP, 则SΔAPB+SΔAPC=SΔABC.
∴ 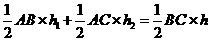 .
.
又 h3=0,AB=AC=BC, ∴ h1+h2+h3==h.
(3)证明:图④中,h1+h2+h3=h.
过点P作RS∥BC与边AB、AC相交于R、S.
在△ARS中,由图②中结论知:h1+h2+0=h-h3.
∴ h1+h2+h3=h.
说明:(2)与(3)问,通过作辅助线,利用证全等三角形的方法类似给分.
(4)h1+h3+h4= 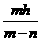 .
.
让R、S延BR、CS延长线向上平移,当n=0时,图⑥变为图④,上面的等式就是图④中的等式,所以上面结论是图④中结论的推广.
11、(2007山东青岛)已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移
动,它们的速度都是1cm/s,当点P到达点B时,P、Q两
点停止运动.设点P的运动时间为t(s),解答下列问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的
关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出相应的t值;不存在,说明理由;
(3)设PQ的长为x(cm),试确定y与x之间的关系式.
解:⑴ 根据题意:AP=t cm,BQ=t cm.
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t ) cm.
△PBQ中,BP=3-t,BQ=t,
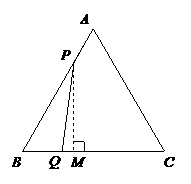 若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
当∠BQP=90°时,BQ=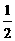 BP.
BP.
即t=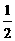 (3-t ),t=1 (秒).
(3-t ),t=1 (秒).
当∠BPQ=90°时,BP=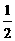 BQ.3-t=
BQ.3-t=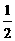 t,t=2 (秒).
t,t=2 (秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
⑵ 过P作PM⊥BC于M .Rt△BPM中,sin∠B=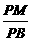 ,
,
∴PM=PB·sin∠B=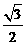 (3-t ).∴S△PBQ=
(3-t ).∴S△PBQ=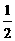 BQ·PM=
BQ·PM=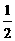 · t ·
· t ·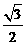 (3-t ).
(3-t ).
∴y=S△ABC-S△PBQ=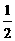 ×32×
×32×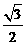 -
-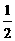 · t ·
· t ·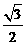 (3-t )=
(3-t )=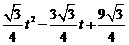 .
.
∴y与t的关系式为: y=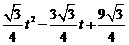 .
.
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的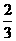 ,
,
则S四边形APQC=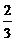 S△ABC .∴
S△ABC .∴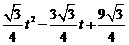 =
=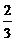 ×
×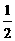 ×32×
×32×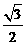 .
.
∴t 2-3 t+3=0.∵(-3) 2-4×1×3<0,∴方程无解.
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的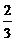 .……8′
.……8′
⑶ 在Rt△PQM中,MQ=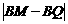 =
=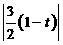 .
.
MQ 2+PM 2=PQ 2.∴x2=[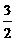 (1-t ) ]2+[
(1-t ) ]2+[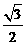 (3-t ) ]2
(3-t ) ]2
=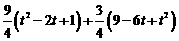 =
=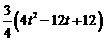 =3t2-9t+9.
=3t2-9t+9.
∴t2-3t=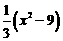 .∵y=
.∵y=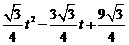 ,
,
∴y=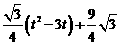 =
=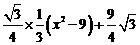 =
=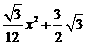 .
.
∴y与x的关系式为:y=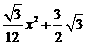 .
.
10、(2007四川乐山)如图(13),在矩形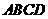 中,
中,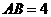 ,
,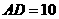 .直角尺的直角顶点
.直角尺的直角顶点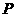 在
在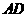 上滑动时(点
上滑动时(点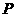 与
与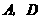 不重合),一直角边经过点
不重合),一直角边经过点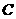 ,另一直角边
,另一直角边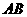 交于点
交于点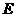 .我们知道,结论“
.我们知道,结论“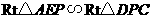 ”成立.
”成立.
(1)当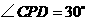 时,求
时,求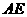 的长;
的长;
 (2)是否存在这样的点
(2)是否存在这样的点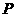 ,使
,使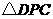 的周长等于
的周长等于 周长的
周长的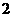 倍?若存在,求出
倍?若存在,求出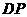 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
我选做的是_____________________.
解(1)在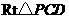 中,由
中,由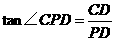 ,
,
得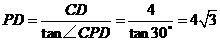
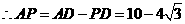 , 由
, 由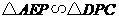 知
知
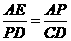 ,
,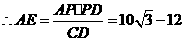 .
.
(2)假设存在满足条件的点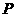 ,设
,设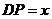 ,则
,则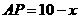
由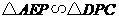 知
知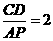 ,
,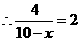 ,解得
,解得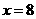 ,
,
 此时
此时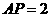 ,
,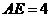 符合题意.
符合题意.
9、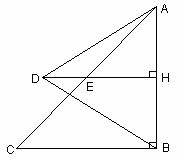 (2007重庆)已知,如图:△ABC是等腰直角三角形,∠ABC=900,AB=10,D为△ABC外一点,边结AD、BD,过D作DH⊥AB,垂足为H,交AC于E。
(2007重庆)已知,如图:△ABC是等腰直角三角形,∠ABC=900,AB=10,D为△ABC外一点,边结AD、BD,过D作DH⊥AB,垂足为H,交AC于E。
(1)若△ABD是等边三角形,求DE的长;
(2)若BD=AB,且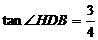 ,求DE的长。
,求DE的长。
解:(1)∵△ABD是等边三角形,AB=10,∴∠ADB=600,AD=AB=10
∵DH⊥AB ∴AH=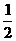 AB=5, ∴DH=
AB=5, ∴DH=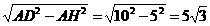
∵△ABC是等腰直角三角形 ∴∠CAB=450
∴∠AEH=450 ∴EH=AH=5,∴DE=DH-EH=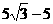
(2)∵DH⊥AB且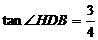 , ∴可设BH=
, ∴可设BH=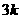 ,则DH=
,则DH=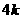 ,DB=
,DB=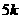
∵BD=AB=10 ∴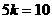 解得:
解得: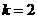
∴DH=8,BH=6,AH=4
又∵EH=AH=4, ∴DE=DH-EH=4
8、 (2007四川乐山)如图(11),在等边
(2007四川乐山)如图(11),在等边 中,点
中,点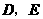 分别在边
分别在边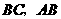 上,且
上,且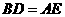 ,
,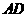 与
与 交于点
交于点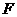 .
.
(1)求证: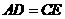 ;
;
(2)求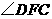 的度数.
的度数.
(1)证明: 是等边三角形,
是等边三角形,
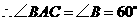 ,
,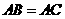
又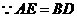
 ,················································································· 4分
,················································································· 4分
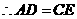 .······································································································· 5分
.······································································································· 5分
(2)解由(1)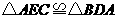 ,
,
得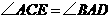 ······························································································· 6分
······························································································· 6分
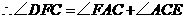
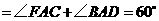 ······················································································ 9分
······················································································ 9分
7、(2007浙江杭州) 如图,已知
如图,已知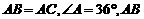 的中垂线
的中垂线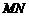 交
交 于点
于点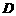 ,交
,交 于点
于点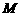 ,有下面4个结论:
,有下面4个结论:
①射线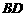 是
是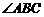 的角平分线;
的角平分线;
②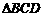 是等腰三角形;
是等腰三角形;
③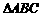 ∽
∽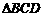 ;
;
④ ≌
≌ 。
。
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明。
(1)正确的结论是①、②、③;(2)证明略。
6、(2007南充)如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由.
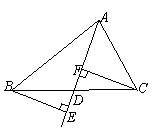

解:AD是△ABC的中线. 理由如下:在Rt△BDE和Rt△CDF中, ∵ BE=CF,∠BDE=∠CDF, ∴ Rt△BDE≌Rt△CDF. ∴ BD=CD. 故AD是△ABC的中线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com