
题目列表(包括答案和解析)
17.(青岛市2008)
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
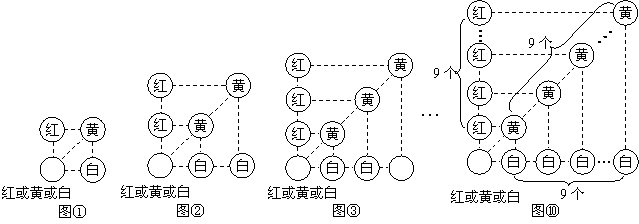
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是: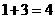 (如图①);
(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是: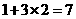 (如图②)
(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是: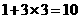 (如图③):
(如图③):

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球
同色,即最少需摸出小球的个数是: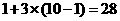 (如图⑩)
(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
(3)若要确保摸出的小球至少有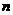 个同色(
个同色(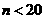 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展二:在不透明口袋中装有 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(2)若要确保摸出的小球至少有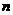 个同色(
个同色(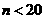 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
16.(湖北省十堰市2008 )
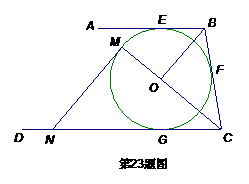
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
⑴求证:MN是⊙O的切线;
⑵当0B=6cm,OC=8cm时,求⊙O的半径及MN的长.
解:⑴证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
∴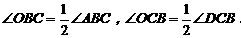
∵AB∥CD,∴∠ABC+∠DCB=180°.
∴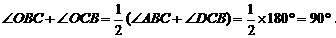
∴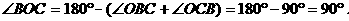
∵MN∥OB,∴∠NMC=∠BOC=90°.∴MN是⊙O的切线.
⑵连接OF,则OF⊥BC.
由⑴知,△BOC是Rt△,∴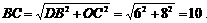
∵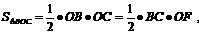
∴6×8=10×OF.∴0F=4.8.
即⊙O的半径为4.8cm.
由⑴知,∠NCM=∠BCO,∠NMC=∠BOC=90°,
∴△NMC∽△BOC.
∴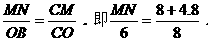
∴MN=9.6(cm).
说明:不带单位不扣分.
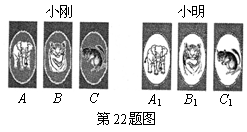
14.(沈阳市2008)小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.
(1)一次出牌小刚出“象”牌的概率是多少?
 (2)如果用
(2)如果用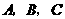 分别表示小刚的象、虎、鼠三张牌,用
分别表示小刚的象、虎、鼠三张牌,用 ,
,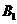 ,
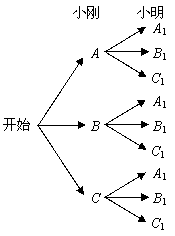
, 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.
分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.
解:(1)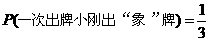
(2)树状图(树形图):

或列表


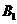


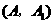
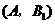
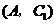
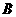
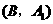
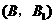
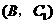
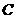
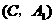
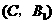
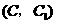
由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种.
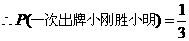 .
.
15(山东省2008)
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;

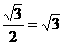 ,BO=2×cos60°=1.
,BO=2×cos60°=1.
在Rt△CBO中,∠CBO=30°,CO=BOtan30°=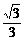 ,
,
∴ CD=DO-CO=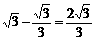 (km).
(km).
即C,D之间的距离为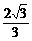 km.
km.
13.(浙江省2008)四川5.12特大地震受灾地区急需大量赈灾帐篷,某帐篷生产企业接到生产任务后,加大生产投入、提高生产效率,实际每天生产帐篷比原计划多200顶,已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同.现在该企业每天能生产多少顶帐篷?
解:设现在该企业每天能生产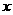 顶帐篷,
顶帐篷,
则原计划每天生产(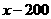 )顶帐篷.
)顶帐篷.
由题意,得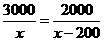 .
.
解得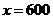 .
.
经检验: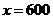 是原方程的解.
是原方程的解.
∴原方程的解是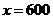 .
.
答:现在该企业每天能生产 顶帐篷.
顶帐篷.
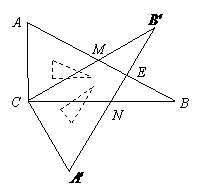
12.(四川省达州市2008)含 角的直角三角板
角的直角三角板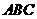 (
(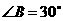 )绕直角顶点
)绕直角顶点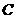 沿逆时针方向旋转角
沿逆时针方向旋转角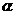 (
(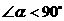 ),再沿
),再沿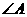 的对边翻折得到
的对边翻折得到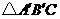 ,
,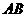 与
与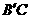 交于点
交于点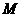 ,
,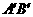 与
与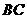 交于点
交于点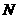 ,
,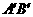 与
与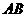 相交于点
相交于点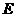 .
.
(1)求证: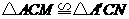 .
.
(2)当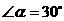 时,找出
时,找出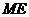 与
与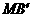 的数量关系,并加以说明.
的数量关系,并加以说明.
(1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
∴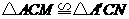
 (2)在Rt△ABC中
(2)在Rt△ABC中
∵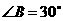 ,∴∠A=900-300=600
,∴∠A=900-300=600
又∵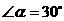 ,∴∠MCN=300,
,∴∠MCN=300,
∴∠ACM=900-∠MCN=600
∴∠EMB′=∠AMC=∠A=∠MCA=600
∵∠B′=∠B=300
所以三角形MEB′是Rt△MEB′且∠B′=300
所以MB′=2ME
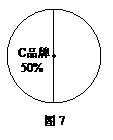
11.(深圳市2008)某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图6和
图7所示的统计图.根据图中信息解答下列问题:
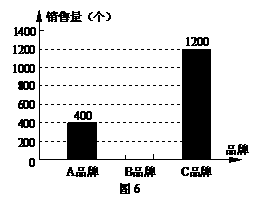
(1)哪一种品牌粽子的销售量最大?
(2)补全图6中的条形统计图.
(3)写出A品牌粽子在图7中所对应的圆心角的度数.
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?
请你提一条合理化的建议.
解: (1)C品牌.(不带单位不扣分)
(2)略.(B品牌的销售量是800个,柱状图上没有标数字不扣分)
(3)60°.(不带单位不扣分)
(4)略.(合理的解释都给分)
10.(青海省西宁市2008)计算: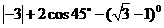 .
.
解:原式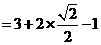 3分
3分
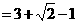
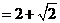
9.(哈尔滨市2008)观察下列图形:

它们是按一定规律排列的,依照此规律,第20个图形共有 60 个★.
7.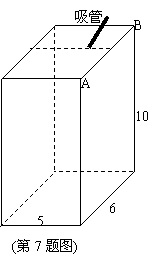 (荆州市2008)如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:㎝),在上盖中开有一孔便于插吸管,吸管长为13㎝, 小孔到图中边AB距离为1㎝,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为h㎝,则h的最小值大约为___2______㎝.(精确到个位,参考数据:
(荆州市2008)如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:㎝),在上盖中开有一孔便于插吸管,吸管长为13㎝, 小孔到图中边AB距离为1㎝,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为h㎝,则h的最小值大约为___2______㎝.(精确到个位,参考数据: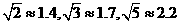 )
)
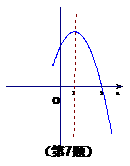 8(常州市2008)已知函数
8(常州市2008)已知函数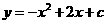 的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.
的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.
6.(2008年南通市) 如图,共有12个大小相同的小正方形,其中阴影部分的5个
小正方形是一个正方体的表面展开图的一部分.现从其余的小
正方形中任取一个涂上阴影,能构成这个正方体的表面展开图
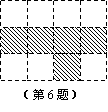 的概率是
的概率是 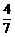 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com