22、(8分)为了进一步了解八年级学生的身体素质情况，体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图．

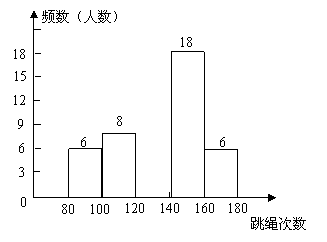如下所示：

组别	次数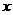	频数(人数)
第1组
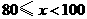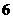第2组
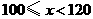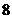第3组
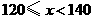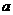第4组
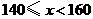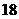第5组

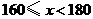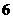请结合图表完成下列问题：

(1)表中的　　　　　 ；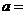

(2)请把频数分布直方图补充完整；

(3)这个样本数据的中位数落在第　　　　 组；

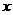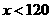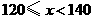(4)若八年级学生一分钟跳绳次数()达标要求是：不合格；为合格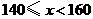；为良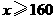；为优．根据以上信息，请你给学校或八年级同学提一条合理化建议：　　　　　　　　　　　　　　　　　　　　　 ．

21、(本题满分7分)

端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一只肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同．小明喜欢吃红枣馅的粽子．

(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；

(2)在吃粽子之前，小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验，规定：掷得点数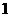向上代表肉馅，点数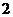向上代表香肠馅，点数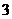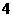，向上代表红枣馅，连续抛掷这个骰子两次表示随机吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率．你认为这样模拟正确吗？试说明理由．

20、(6分)如图，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC， 可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷。经过了解，教学楼、水塔的高分别为20m和30m，它们之间的距离为30m，小张身高为1.6m。小张要想看到水塔，他与教学楼的距离至少应有多少m？

19、(9分)如图，在平面直角坐标系中，将四边形ABCD称为“基本图形”，且各点的坐标分别为A(4，4)，B(1，3)，C(3，3)，D(3，1).

(1)画出“基本图形”关于原点O对称的四边形A₁B₁C₁D₁，并求出A₁，B₁，C₁，D₁ 的坐标.

A₁(　　 ，　　 )，B₁(　　 ，　　 )，C₁(　　 ，　　 )，D₁(　　 ，　　 ) ；

(2)画出“基本图形”关于x轴的对称图形A₂B₂C₂D₂ ；

　(3)画出四边形A₃B₃C₃D₃，使之与前面三个图形组成的图形既是中心对称图形又

　　　 轴对称图形.

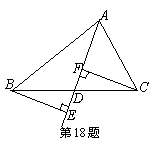
18、(6分)如图，已知BE⊥AD，CF⊥AD，且BE＝CF．请你判断AD是△ABC的中线还是角平分线？请说明你判断的理由．

17、(6分)在解题目：“当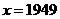时，求代数式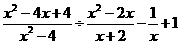的值”时，聪聪认为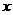只要任取一个使原式有意义的值代入都有相同结果．你认为他说的有理吗？请说明理由．

16、(6分)计算：(－2^－2 +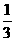)×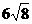－2009⁰÷sin 45°．

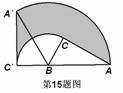
15、如图，在Rt△ABC中，∠BCA=90⁰，∠BAC = 30⁰，AB=8cm，把△ABC以

点B为中心，逆时针旋转使点C旋转到AB边的延长线上点C`处，求AC边扫

过的图形(图中阴影部分)的面积为_________cm.。(结果保留∏)

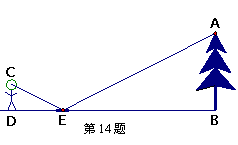
14、为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下　 的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在离树底(B)8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树AB的高度为 　　　米．

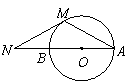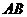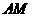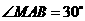13、如图，是⊙O的直径，为弦，，过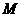

点的⊙O的切线交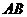延长线于点_，则⊙O的半

　径为　　　　 cm．