
题目列表(包括答案和解析)
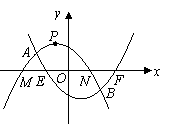
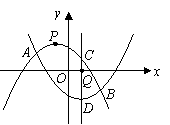
25.(08江西南昌)24.如图,抛物线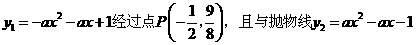 相交于
相交于 两点.
两点.
(1)求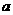 值;
值;
(2)设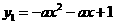 与
与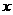 轴分别交于
轴分别交于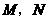 两点(点
两点(点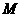 在点
在点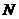 的左边),
的左边),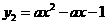 与
与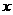 轴分别交于
轴分别交于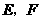 两点(点
两点(点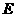 在点
在点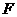 的左边),观察
的左边),观察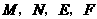 四点的坐标,写出一条正确的结论,并通过计算说明;
四点的坐标,写出一条正确的结论,并通过计算说明;
 (3)设
(3)设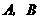 两点的横坐标分别记为
两点的横坐标分别记为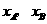 ,若在
,若在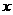 轴上有一动点
轴上有一动点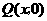 ,且
,且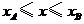 ,过
,过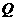 作一条垂直于
作一条垂直于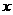 轴的直线,与两条抛物线分别交于C,D两点,试问当
轴的直线,与两条抛物线分别交于C,D两点,试问当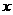 为何值时,线段CD有最大值?其最大值为多少?
为何值时,线段CD有最大值?其最大值为多少?
(08江西南昌24题解析)24.解:(1) 点
点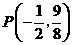 在抛物线
在抛物线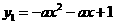 上,
上,
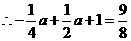 ,··························································································· 2分
,··························································································· 2分
解得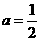 .··········································································································· 3分
.··········································································································· 3分
(2)由(1)知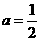 ,
, 抛物线
抛物线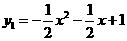 ,
,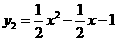 .······· 5分
.······· 5分
 当
当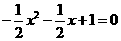 时,解得
时,解得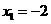 ,
,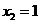 .
.
 点
点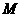 在点
在点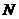 的左边,
的左边,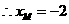 ,
,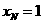 .············ 6分
.············ 6分
当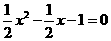 时,解得
时,解得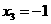 ,
,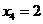 .
.
 点
点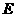 在点
在点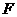 的左边,
的左边,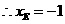 ,
,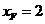 .························································ 7分
.························································ 7分
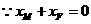 ,
,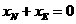 ,
,
 点
点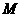 与点
与点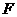 对称,点
对称,点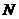 与点
与点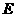 对称.······························································· 8分
对称.······························································· 8分
 (3)
(3)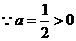 .
.
 抛物线
抛物线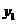 开口向下,抛物线
开口向下,抛物线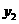 开口向上.················ 9分
开口向上.················ 9分
根据题意,得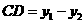
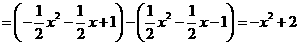 .··············································· 11分
.··············································· 11分
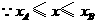 ,
, 当
当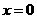 时,
时,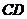 有最大值
有最大值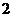 .··············································· 12分
.··············································· 12分
说明:第(2)问中,结论写成“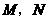 ,
,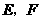 四点横坐标的代数和为0”或“
四点横坐标的代数和为0”或“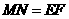 ”均得1分.
”均得1分.
49.(08四川宜宾)24、(本小题满分12分)
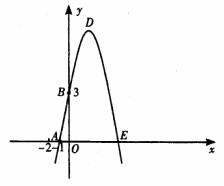
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1) 求该抛物线的解析式;
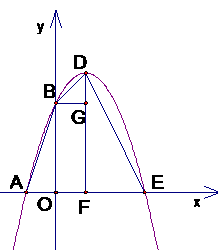
(2) 若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3) △AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为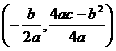 )
)
(08四川宜宾24题解析)24.解:( 1)由已知得:
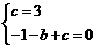 解得
解得
c=3,b=2
 ∴抛物线的线的解析式为
∴抛物线的线的解析式为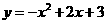
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=
=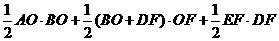
=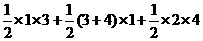
=9
(3)相似
如图,BD=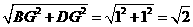
BE=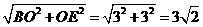
DE=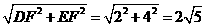
所以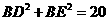 ,
, 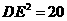 即:
即: 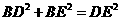 ,所以
,所以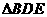 是直角三角形
是直角三角形
所以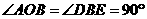 ,且
,且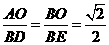 ,
,
所以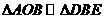 .
.
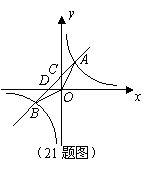
48.(08四川内江)(本题答案暂缺)21.(9分)如图,一次函数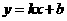 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于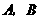 两点,与
两点,与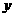 轴交于点
轴交于点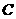 ,与
,与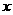 轴交于点
轴交于点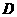 ,
,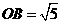 .且点
.且点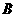 横坐标是点
横坐标是点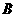 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
 (2)设点
(2)设点 横坐标为
横坐标为 ,
,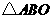 面积为
面积为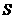 ,求
,求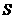 与
与 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.
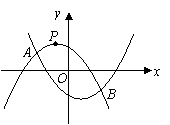
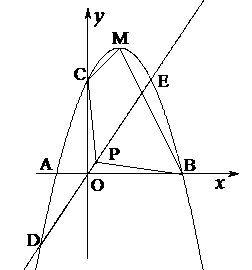
9.如图11,已知二次函数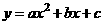 的图像经过三点A
的图像经过三点A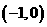 ,B
,B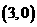 ,C
,C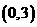 ,它的顶点为M,又正比例函数
,它的顶点为M,又正比例函数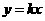 的图像于二次函数相交于两点D、E,且P是线段DE的中点。
的图像于二次函数相交于两点D、E,且P是线段DE的中点。
⑴求该二次函数的解析式,并求函数顶点M的坐标;
⑵已知点E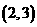 ,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量
,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量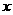 的取值范围;
的取值范围;
⑶当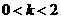 时,求四边形PCMB的面积
时,求四边形PCMB的面积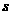 的最小值。
的最小值。
[参考公式:已知两点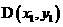 ,
,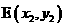 ,则线段DE的中点坐标为
,则线段DE的中点坐标为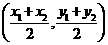 ]
]
47.(08四川泸州)(本题答案暂缺)四(本大题 10分)
46.(08四川凉山)25.(9分)如图,在 中
中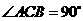 ,
,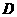 是
是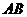 的中点,以
的中点,以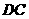 为直径的
为直径的 交
交 的三边,交点分别是
的三边,交点分别是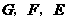 点.
点.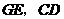 的交点为
的交点为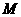 ,且
,且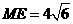 ,
, .
.
(1)求证: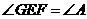 .
.
(2)求 的直径
的直径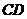 的长.
的长.
 (3)若
(3)若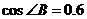 ,以
,以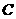 为坐标原点,
为坐标原点,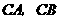 所在的直线分别为
所在的直线分别为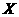 轴和
轴和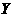 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线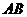 的函数表达式.
的函数表达式.
(08四川凉山25题解析)25.(9分)
(1)连接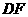
 是圆直径,
是圆直径,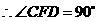 ,即
,即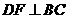
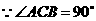 ,
,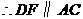 .················································································· 1分
.················································································· 1分
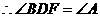 .
. 在
在 中
中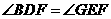 ,
,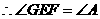 .··························· 2分
.··························· 2分
(2)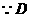 是
是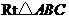 斜边
斜边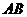 的中点,
的中点,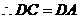 ,
, ,
,
又由(1)知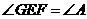 ,
,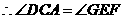 .
.
又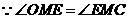 ,
,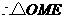 与
与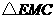 相似······················································ 3分
相似······················································ 3分
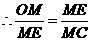
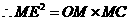 ············································································ 4分
············································································ 4分
又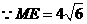 ,
,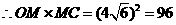
 ,
,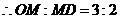 ,
,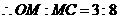 ······································ 5分
······································ 5分
设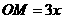 ,
,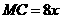 ,
,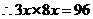 ,
,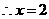
 直径
直径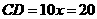 .······························································································· 6分
.······························································································· 6分
(3) 斜边上中线
斜边上中线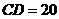 ,
,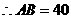
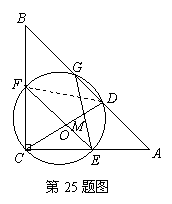
 在
在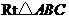 中
中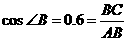 ,
,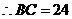 ,
,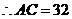 ······························ 7分
······························ 7分
设直线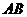 的函数表达式为
的函数表达式为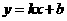 ,
,
根据题意得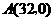 ,
,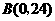
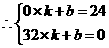 解得
解得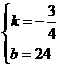
 直线
直线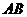 的函数解析式为
的函数解析式为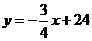 (其他方法参照评分)································· 9分
(其他方法参照评分)································· 9分
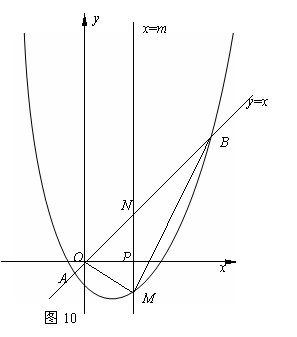
25.如图10,已知抛物线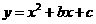 经过点(1,-5)和(-2,4)
经过点(1,-5)和(-2,4)
(1)求这条抛物线的解析式.
(2)设此抛物线与直线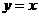 相交于点A,B(点B在点A的右侧),平行于
相交于点A,B(点B在点A的右侧),平行于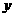 轴的直线
轴的直线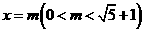 与抛物线交于点M,与直线
与抛物线交于点M,与直线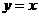 交于点N,交
交于点N,交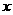 轴于点P,求线段MN的长(用含
轴于点P,求线段MN的长(用含 的代数式表示).
的代数式表示).
(3)在条件(2)的情况下,连接OM、BM,是否存在 的值,使△BOM的面积S最大?若存在,请求出
的值,使△BOM的面积S最大?若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
43.(08四川广安)(本题答案暂缺)七、解答题(本大题满分12分)
28. 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且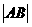 =3
=3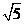 ,sin∠OAB=
,sin∠OAB=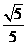 .
.
(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的函数表达式;
(2)在(1)中,抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将点O、点A分别变换为点Q( -2k ,0)、点R(5k,0)(k>1的常数),设过Q、R两点,且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N,其顶点为M,记△QNM的面积为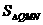 ,△QNR的面积
,△QNR的面积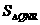 ,求
,求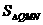 ∶
∶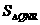 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com