
题目列表(包括答案和解析)
5、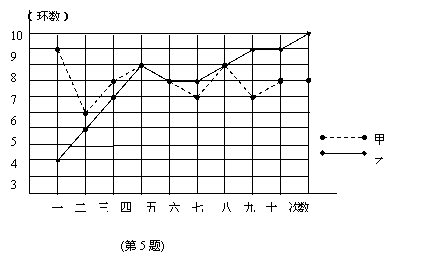 (河北02)甲、乙两人在相同
(河北02)甲、乙两人在相同
条件下各射靶10次,每次射靶
的面绩情况如图所示.
(1)请填写下表:
|
|
平均数 |
方差 |
中位数 |
命中9环比上次数 |
|
甲 |
7 |
1.2 |
|
1 |
|
乙 |
|
5.4 |
|
|
(2)请从下列四个不同的角度对这次测试结果进行分析.
①从平均数和方差相结合看:
②从平均数和中位数相结合看(分析谁的成绩好些):
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些):
④从折线图上两人射击命中环数的走势看(分析谁更有潜力):
4、(河北实验区06)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
|
员工 |
管理人员 |
普通工作人员 |
|||||
|
人员结构 |
总经理 |
部门经理 |
科研人员 |
销售人员 |
高级技工 |
中级技工 |
勤杂工 |
|
员工数/名 |
1 |
3 |
2 |
3 |
 |
24 |
1 |
|
每人月工资/元 |
21000 |
8400 |
2025 |
2200 |
1800 |
1600 |
950 |
 请你根据上述内容,解答下列问题:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数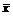 为2500元,
为2500元,
中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.
请你回答右图中小张的问题,并指
出用(2)中的哪个数据向小张介绍
员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资 (结果保留整数),并判断
(结果保留整数),并判断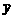 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
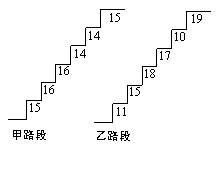
3、(河北实验区04)在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差
和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
 (3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不娈的情况下,请你提出
合理的整修建议.
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不娈的情况下,请你提出
合理的整修建议.
2、(04河北)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动.初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
|
|
决赛成绩(单位:分) |
|
初一年级 |
80 86 88 80 88 99 80 74 91 89 |
|
初二年级 |
85 85 87 97 85 76 88 77 87 88 |
|
初三年级 |
82
80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
|
|
平均数 |
众数 |
中位数 |
|
初一年级 |
85.5 |
|
87 |
|
初二年级 |
85.5 |
85 |
|
|
初三年级 |
|
|
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
① 从平均数和众数相结合看(分析哪个年级成绩好些);
② 从平均数和中位数相结合看(分析哪个年级成绩好些).
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?并说明理由.
1、(08太原)用商家免费提供的塑料袋购物,我们享受着方便和快捷,但同时要关注它对环境的潜在危害.为了解太原市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:
|
每户丢弃塑料袋数(单位:个) |
1 |
2 |
3 |
4 |
5 |
6 |
|
家庭数(单位:户) |
15 |
60 |
65 |
35 |
20 |
5 |
(1)求这天这200户家庭平均每户丢弃塑料袋的个数.
(2)假设我市现有家庭100万户,据此估计全市所有家庭每年(以365天计算)丢弃塑料袋的总数.
(3)下图是我市行政区划图,它的面积相当于图中 的面积.已知
的面积.已知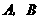 间的实际距离为150km,
间的实际距离为150km,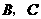 间的实际距离为110km,
间的实际距离为110km,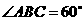 .根据(2)中的估算结果,求我市每年每平方公里的土地上会增加多少个塑料袋?(取
.根据(2)中的估算结果,求我市每年每平方公里的土地上会增加多少个塑料袋?(取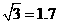 ,
, 的面积和最后计算结果都精确到千位)
的面积和最后计算结果都精确到千位)
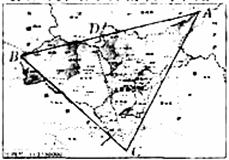
“问题”是数学的心脏,而“问题解决”又是数学的永恒主题,在学习数学知识的同时,亲身参与到“问题解决”的实践过程之中,从而提高其数学思维能力。
例4. 已知△ABC中,AB=c,BC=a,CA=b,且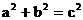 ,求证:∠C=90°
,求证:∠C=90°
分析:作△A’B’C’,使∠C=90°,B’C’=a,A’C’=b
则由条件及勾股定理得: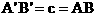
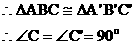
例5. 如图, 中,∠1=90°,AB=13,BC=12,D在△ABC外,且AD=4,CD=3,求证:∠D=90°
中,∠1=90°,AB=13,BC=12,D在△ABC外,且AD=4,CD=3,求证:∠D=90°
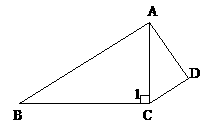
分析:先用勾股定理求出AC,再用逆定理求得∠D=90°,详细过程请同学们自己完成。
注:上面两例的结论是类似的。但证明的方法显然不同,即问题解决的方法不同,例4是构造法,例5直接用定理。
数学方法是多种多样的,限于篇幅,这里先谈这么多,只要同学们留心观察,细心体会,就一定能把数学学好。
数学知识是一个有机整体,许多知识点都有着内在的辩证统一的联系。如“勾股定理的逆定理”是在“勾股定理”的基础上形成的,两个定理不但组成了一对完美的互逆定理,而且在其研究过程中亦体现了数学知识内在发展运动的辩证统一思想。
例3. 如图,△ABC中,D在AB上,且CD为AB边上的高。
(1)若∠ACB=90°,求证: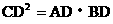 ;
;
(2)若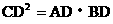 ,求证:∠ACB=90°。
,求证:∠ACB=90°。
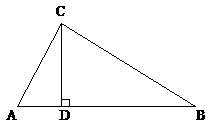
分析:(1)、(2)两问条件与结论互换,看似一个题目,一个用正定理,一个用逆定理。此题一定要注意图和条件,D若在AB外,就无(2)这个结论了。详细证明过程请同学们自己完成。
分类讨论是一种很重要的数学方法。分类讨论法(亦称穷举法或枚举法),具体地说,就是我们要解决一个复杂的问题时,常把讨论的对象分成若干种(为数不多的)情况,然后对各种情况逐个讨论,最终解决整个问题。
例2. 某商店的糖果有3千克和5千克两种包装,货源充足,保证供应。
求证:凡购买N(N是大于等于8的自然数)千克糖果时,都不必拆包。
分析:把问题“数学化”。对任意自然数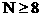 ,一定存在非负整数m,n,使得
,一定存在非负整数m,n,使得 。下面对N分三类讨论。
。下面对N分三类讨论。
①当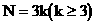 ,只需给顾客k包3千克装的即可。
,只需给顾客k包3千克装的即可。
②当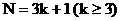
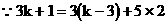
∴给顾客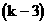 包3千克装的及2包5千克装的糖果即可。
包3千克装的及2包5千克装的糖果即可。
③当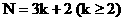
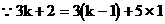
∴给顾客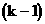 包3千克装的及1包5千克装的糖果即可
包3千克装的及1包5千克装的糖果即可
数学建模思想是联系数学与现实的桥梁,是学生领悟数学来源于生活又还原于生活的重要途径,使其真正体会到学以致用的意义。
例1. 桌上有7只茶杯,杯口全部朝上,每次“运动”是指将其中4只茶杯同时翻转,问:能否经过若干次运动使杯口全部朝下?
分析:把问题“数字化”,将杯口朝上的茶杯记作+1,杯口朝下的茶杯记作-1。则全部朝上状态为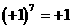 ,全部朝下状态为
,全部朝下状态为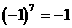 。每次将4只茶杯同时翻转,即将要改变4个符号,即
。每次将4只茶杯同时翻转,即将要改变4个符号,即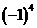 ,但
,但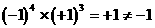 。所以不论经过多少次运动,杯口全部朝下都是不可能的。
。所以不论经过多少次运动,杯口全部朝下都是不可能的。
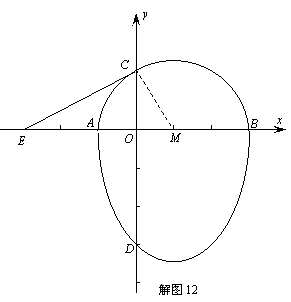
24.解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为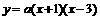 (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,解之得:a=1
∴y=x2-2x-3····································································································· 3分
自变量范围:-1≤x≤3···················································································· 4分
解法2:设抛物线的解析式为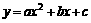 (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点都在抛物线上
∴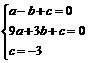 ,解之得:
,解之得: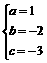
∴y=x2-2x-3····································································································· 3分
自变量范围:-1≤x≤3······························································ 4分
(2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,
在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=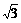
在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0,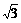 ),(-3,0) ·················································· 6分
),(-3,0) ·················································· 6分
∴切线CE的解析式为 ··························································· 8分
··························································· 8分
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ·························· 9分
由题意可知方程组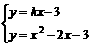 只有一组解
只有一组解
即 有两个相等实根,∴k=-2·············································· 11分
有两个相等实根,∴k=-2·············································· 11分
∴过点D“蛋圆”切线的解析式y=-2x-3····················································· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com