
题目列表(包括答案和解析)
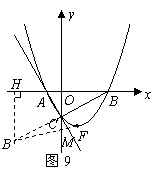
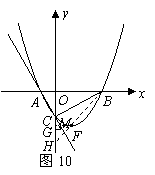
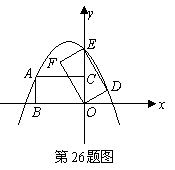
84.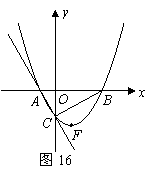 (08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线
(08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线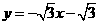 与
与 轴交于点
轴交于点 ,与
,与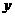 轴交于点
轴交于点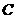 ,抛物线
,抛物线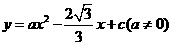 经过
经过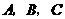 三点.
三点.
(1)求过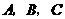 三点抛物线的解析式并求出顶点
三点抛物线的解析式并求出顶点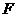 的坐标;
的坐标;
(2)在抛物线上是否存在点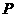 ,使
,使 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出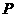 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)试探究在直线 上是否存在一点
上是否存在一点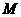 ,使得
,使得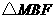 的周长最小,若存在,求出
的周长最小,若存在,求出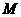 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(08辽宁12市26题解析)
解:(1) 直线
直线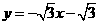 与
与 轴交于点
轴交于点 ,与
,与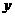 轴交于点
轴交于点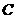 .
.
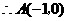 ,
,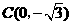 ························································································· 1分
························································································· 1分
 点
点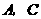 都在抛物线上,
都在抛物线上,
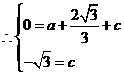
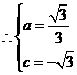
 抛物线的解析式为
抛物线的解析式为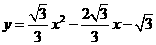 ························································ 3分
························································ 3分
 顶点
顶点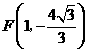 ······························································································· 4分
······························································································· 4分
(2)存在··············································································································· 5分
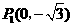 ············································································································· 7分
············································································································· 7分
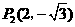 ············································································································ 9分
············································································································ 9分
(3)存在·············································································································· 10分
理由:
解法一:
延长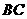 到点
到点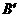 ,使
,使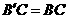 ,连接
,连接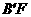 交直线
交直线 于点
于点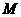 ,则点
,则点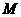 就是所求的点.
就是所求的点.
····················································································· 11分
 过点
过点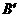 作
作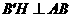 于点
于点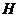 .
.
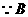 点在抛物线
点在抛物线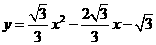 上,
上,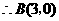
在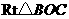 中,
中,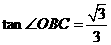 ,
,
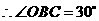 ,
,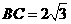 ,
,
在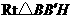 中,
中,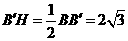 ,
,
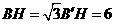 ,
,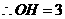 ,
,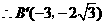 ··············································· 12分
··············································· 12分
设直线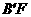 的解析式为
的解析式为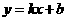
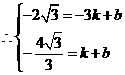 解得
解得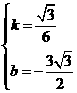
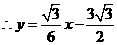 ································································································ 13分
································································································ 13分
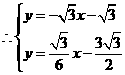 解得
解得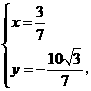
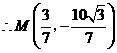
 在直线
在直线 上存在点
上存在点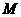 ,使得
,使得 的周长最小,此时
的周长最小,此时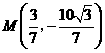 .··· 14分
.··· 14分
解法二:
 过点
过点 作
作 的垂线交
的垂线交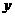 轴于点
轴于点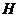 ,则点
,则点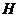 为点
为点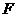 关于直线
关于直线 的对称点.连接
的对称点.连接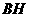 交
交 于点
于点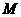 ,则点
,则点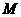 即为所求.················································································ 11分
即为所求.················································································ 11分
过点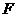 作
作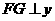 轴于点
轴于点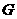 ,则
,则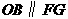 ,
,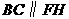 .
.
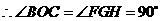 ,
,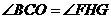
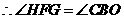
同方法一可求得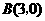 .
.
在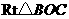 中,
中,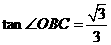 ,
,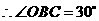 ,可求得
,可求得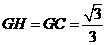 ,
,
 为线段
为线段 的垂直平分线,可证得
的垂直平分线,可证得 为等边三角形,
为等边三角形,
 垂直平分
垂直平分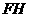 .
.
即点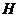 为点
为点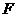 关于
关于 的对称点.
的对称点.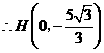 ············································· 12分
············································· 12分
设直线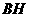 的解析式为
的解析式为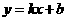 ,由题意得
,由题意得
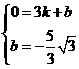 解得
解得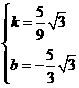
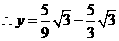 ································································································ 13分
································································································ 13分
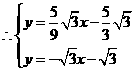 解得
解得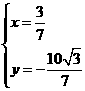
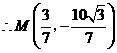
 在直线
在直线 上存在点
上存在点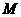 ,使得
,使得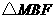 的周长最小,此时
的周长最小,此时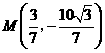 .··· 14分
.··· 14分
83. (08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形
(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形 的边
的边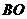 在
在 轴的负半轴上,边
轴的负半轴上,边 在
在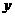 轴的正半轴上,且
轴的正半轴上,且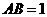 ,
,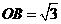 ,矩形
,矩形 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转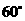 后得到矩形
后得到矩形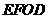 .点
.点 的对应点为点
的对应点为点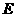 ,点
,点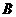 的对应点为点
的对应点为点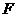 ,点
,点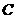 的对应点为点
的对应点为点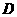 ,抛物线
,抛物线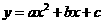 过点
过点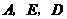 .
.
(1)判断点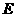 是否在
是否在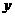 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在 轴的上方是否存在点
轴的上方是否存在点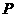 ,点
,点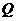 ,使以点
,使以点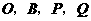 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形 面积的2倍,且点
面积的2倍,且点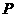 在抛物线上,若存在,请求出点
在抛物线上,若存在,请求出点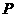 ,点
,点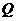 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08辽宁沈阳26题解析)解:(1)点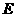 在
在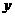 轴上················································· 1分
轴上················································· 1分
理由如下:
连接 ,如图所示,在
,如图所示,在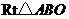 中,
中,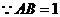 ,
,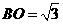 ,
,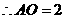
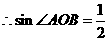 ,
,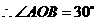
由题意可知: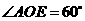
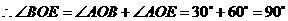
 点
点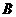 在
在 轴上,
轴上, 点
点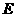 在
在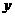 轴上.········································································· 3分
轴上.········································································· 3分
(2)过点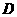 作
作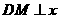 轴于点
轴于点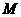
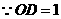 ,
,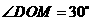
 在
在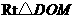 中,
中,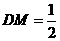 ,
,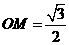
 点
点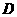 在第一象限,
在第一象限,
 点
点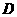 的坐标为
的坐标为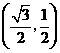 ·························································································· 5分
·························································································· 5分
由(1)知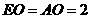 ,点
,点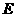 在
在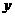 轴的正半轴上
轴的正半轴上
 点
点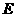 的坐标为
的坐标为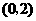
 点
点 的坐标为
的坐标为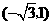 ···························································································· 6分
···························································································· 6分
 抛物线
抛物线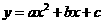 经过点
经过点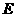 ,
,
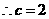
由题意,将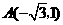 ,
,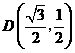 代入
代入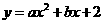 中得
中得
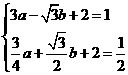 解得
解得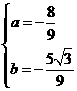
 所求抛物线表达式为:
所求抛物线表达式为: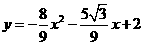 ······················································· 9分
······················································· 9分
(3)存在符合条件的点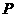 ,点
,点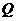 .········································································· 10分
.········································································· 10分
理由如下: 矩形
矩形 的面积
的面积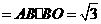
 以
以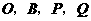 为顶点的平行四边形面积为
为顶点的平行四边形面积为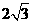 .
.
由题意可知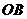 为此平行四边形一边,
为此平行四边形一边,
又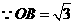
 边上的高为2··································································································· 11分
边上的高为2··································································································· 11分
依题意设点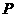 的坐标为
的坐标为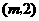
 点
点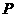 在抛物线
在抛物线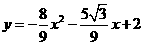 上
上
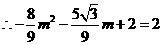
解得,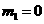 ,
,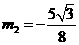
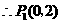 ,
,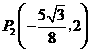
 以
以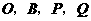 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
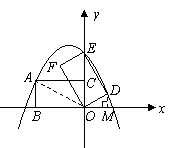
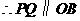 ,
,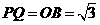 ,
,
 当点
当点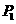 的坐标为
的坐标为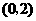 时,
时,
点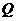 的坐标分别为
的坐标分别为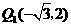 ,
,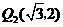 ;
;
当点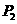 的坐标为
的坐标为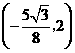 时,
时,
点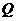 的坐标分别为
的坐标分别为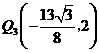 ,
,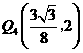 .··············································· 14分
.··············································· 14分
82.(08广东肇庆25题)(本小题满分10分)
已知点A(a,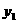 )、B(2a,y
)、B(2a,y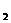 )、C(3a,y
)、C(3a,y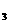 )都在抛物线
)都在抛物线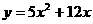 上.
上.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积;
(3)是否存在含有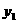 、y
、y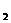 、y
、y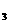 ,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
(08广东肇庆25题解析)(本小题满分10分)
解:(1)由5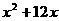 =0,·············································································· (1分)
=0,·············································································· (1分)
得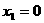 ,
,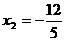 .·················································································· (2分)
.·················································································· (2分)
∴抛物线与x轴的交点坐标为(0,0)、(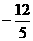 ,0).······································· (3分)
,0).······································· (3分)
(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),······························ (4分)
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,则有
 =S
=S -
- -
- ···················································· (5分)
···················································· (5分)
=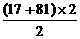 -
-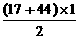 -
-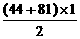 ···································· (6分)
···································· (6分)
=5(个单位面积)········································································ (7分)
(3)如: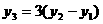 . ········································································· (8分)
. ········································································· (8分)
事实上,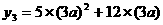 =45a2+36a.
=45a2+36a.
3(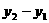 )=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)
)=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)
∴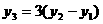 . ···················································································· (10分)
. ···················································································· (10分)
81.(08广东茂名25题)(本题满分10分)
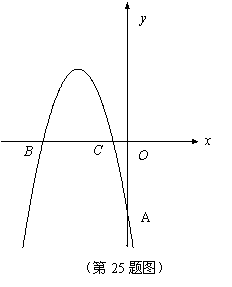 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线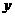 =-
=-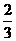

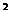 +
+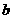
 +
+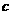 经过A(0,-4)、B(
经过A(0,-4)、B(
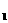 ,0)、 C(
,0)、 C(
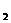 ,0)三点,且
,0)三点,且
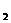 -
-
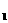 =5.
=5.
(1)求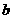 、
、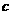 的值;(4分)
的值;(4分)
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对 角线的菱形;(3分)
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)
解:
(08广东茂名25题解析)解:(1)解法一:
∵抛物线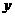 =-
=-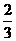

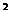 +
+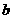
 +
+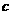 经过点A(0,-4),
经过点A(0,-4),
∴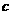 =-4 ……1分
=-4 ……1分
又由题意可知,
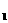 、
、
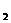 是方程-
是方程-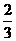

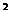 +
+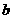
 +
+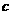 =0的两个根,
=0的两个根,
∴
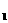 +
+
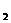 =
=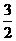
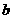 ,
,

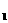

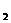 =-
=-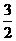
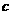 =6··································································· 2分
=6··································································· 2分
由已知得(
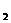 -
-
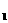 )
)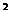 =25
=25
又(
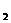 -
-
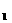 )
)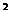 =(
=(
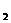 +
+
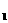 )
)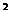 -4
-4
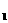

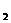 =
=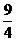
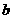
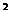 -24
-24
∴ 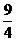
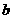
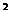 -24=25
-24=25
解得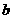 =±
=±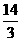 ··········································································································· 3分
··········································································································· 3分
当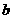 =
=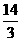 时,抛物线与
时,抛物线与 轴的交点在
轴的交点在 轴的正半轴上,不合题意,舍去.
轴的正半轴上,不合题意,舍去.
∴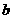 =-
=-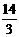 . ·········································································································· 4分
. ·········································································································· 4分
解法二:∵
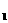 、
、
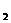 是方程-
是方程-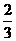

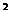 +
+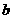
 +c=0的两个根,
+c=0的两个根,
即方程2
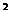 -3
-3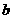
 +12=0的两个根.
+12=0的两个根.
∴ =
=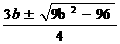 ,··········································································· 2分
,··········································································· 2分
∴
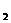 -
-
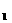 =
=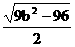 =5,
=5,
解得 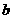 =±
=±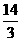 ······························································································· 3分
······························································································· 3分
(以下与解法一相同.)
(2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上, 5分
又∵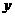 =-
=-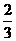

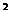 -
-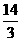
 -4=-
-4=-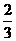 (
( +
+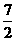 )
)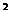 +
+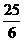 ································· 6分
································· 6分
∴抛物线的顶点(-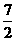 ,
,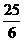 )即为所求的点D.······································· 7分
)即为所求的点D.······································· 7分
(3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0),
根据菱形的性质,点P必是直线 =-3与
=-3与
抛物线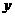 =-
=-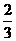

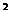 -
-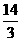
 -4的交点, ···························································· 8分
-4的交点, ···························································· 8分
∴当 =-3时,
=-3时,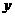 =-
=-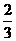 ×(-3)
×(-3) -
-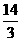 ×(-3)-4=4,
×(-3)-4=4,
∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形. ·················· 9分
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上.······································································································· 10分
有理数的加减,打破了小学数学中的加与减的严格界限,把加、减统一成加法。这都是由于引进了负数,也正是由于引进了负数,小学时我们所熟悉的许多结论在有理数范围内都不一定成立了。下面的几个问题作为本文的结尾,请同学们认真思考并做出回答:
(1)“两个数相加,和一定大于或等于各个加数”吗?
(2)“两个数相减,差一定小于或等于被减数”吗?
(3)“一个数的3倍一定大于这个数的2倍”吗?
在初次进行有理数的加减运算时,首先要分清“+”、“-”号是运算符号还是性质符号。刚开始时,最好把性质符号用括号括起来,使性质符号与运算符号分开。如:正2加上负3,应写作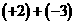 ,不能写成“
,不能写成“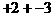 ”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。
”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。
在小学数学中,“+”、“-”表示加号和减号。学习有理数后,“+”与“-”还表示正号与负号。
我们通常把四则运算中的加(+)、减(-)、乘(×)、除(÷)号叫运算符号;把表示正负数的正(+)、负(-)号叫性质符号。另外,负(-)号除了表示上述两种意义外,还表示一个数的相反数。如:-5可表示为5的相反数,而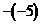 ,表示
,表示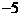 的相反数。
的相反数。
例7. 已知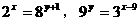 ,试求
,试求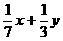 的值。
的值。
剖析:欲求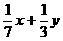 的值,只有先求得x、y的值。为此必须逆用幂的运算法则,把已知等式化为同底数幂,由指数相等列出方程组求解。
的值,只有先求得x、y的值。为此必须逆用幂的运算法则,把已知等式化为同底数幂,由指数相等列出方程组求解。
解:把已知等式化为同底数幂,得:
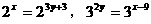
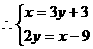
解之得: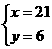
∴原式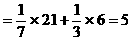
4. 用于比较大小
例6. 比较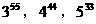 的大小。
的大小。
解: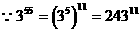
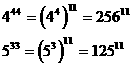
显然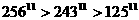
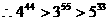
评注:例4中如果按有理数运算顺序计算是十分繁杂的,而逆用法则却极为方便;例5通过逆用法则,也简便获解;例3、例6直接求解,很难进行,但逆用幂的运算法则,问题就迎刃而解,足见适时逆用法则的巨大威力。
3. 用于求值
例5. 已知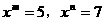 ,求
,求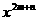 的值。
的值。
解:原式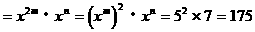
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com