
题目列表(包括答案和解析)
3、 求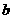 、
、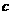 的值;
的值;
5、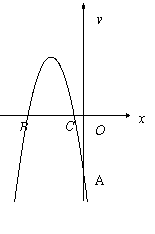 (08茂名市)如图,在平面直角坐标系中,抛物线
(08茂名市)如图,在平面直角坐标系中,抛物线 =-
=-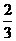
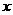
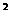 +
+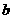
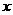 +
+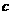 经过A(0,-4)、B(
经过A(0,-4)、B(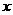
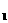 ,0)、 C(
,0)、 C(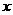
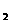 ,0)三点,且
,0)三点,且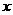
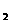 -
-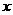
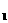 =5.
=5.
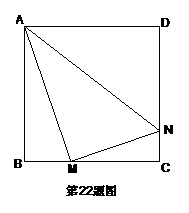
4、 (08茂名市)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(08茂名市)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;(3分)
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分)
(3)当AB=5,BC=6时,求⊙O的半径.(4分)

3、(10广东省)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2。动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动。连接FM、FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒。试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?当x在何范围时,△PQW不为直角三角形?
 (3)问当x为何值时,线段MN最短?求此时MN的值。
(3)问当x为何值时,线段MN最短?求此时MN的值。

2、(09广东省) 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
 (2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM ∽Rt△AMN,
求此时x的值.
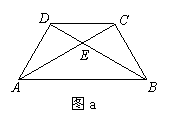
1、(08广东省)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
(1)填空:如图a,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图a中所有的相似三角形(不含全等三角形).
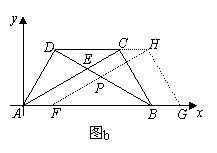 (3)如图b,若以AB所在直线为
(3)如图b,若以AB所在直线为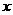 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为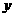 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向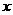 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
3.考试时不能使用计算器,所有答案都必须做在答题卷标定的位置上,请务必注意标角、连线等均要求在答题卷上。
2.答题时, 应该在答题卷指定位置写明校名、 姓名、班级和考试序号等。
1. 本试卷分试题卷和答题卷两部分。满分120分, 考试时间120分钟,本次考试采用闭卷形式。
(三)、解答题
11.(08.湖北)如图,利用一面墙(墙的长度不超过45m),用80 m长的篱笆围一个矩形场地。
 (1)怎样围才能使矩形场地的面积为750 m2?
(1)怎样围才能使矩形场地的面积为750 m2?
(2)能否使所围矩形场地的面积为810 m2,为什么?
12. (10内江市)一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
|
销售方式 |
粗加工后销售 |
精加工后销售 |
|
每吨获利(元) |
1000 |
2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
13.(08年鄂州市)某货运码头,有稻谷和棉花共2680t,其中稻谷比棉花多380t.
(1)求稻谷和棉花各是多少?
(2)现安排甲、乙两种不同规格的集装箱共50个,将这批稻谷和棉花运往外地.已知稻谷35t和棉花15t可装满一个甲型集装箱;稻谷25t和棉花35t可装满一个乙型集装箱.按此要求安排甲、乙两种集装箱的个数,有哪几种方案?
14.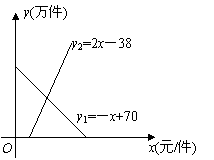 (2010.十堰)如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(2010.十堰)如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量(2)价格在什么范围内,该
药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
15.自2008年爆发全球金融危机以来,部分企业受到了不同程度的影响,为落实“促民生、促经济”政策,济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额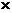 销售的件数)。如下表所示甲、乙两位职工今年五月份的工资情况信息:
销售的件数)。如下表所示甲、乙两位职工今年五月份的工资情况信息:
|
职工 |
甲 |
乙 |
|
月销售件数(件) |
200 |
1800 |
|
月工资(元) |
1800 |
1700 |
(1)试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元?
(2)若职工丙今年六月份的工资不低于2000元,那么丙该月至少应销售多少件产品?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com