
题目列表(包括答案和解析)
(二)、填空题
5. (10泉州市)在一次函数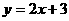 中,
中,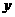 随
随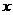 的增大而 (填“增大”或“减小”),当
的增大而 (填“增大”或“减小”),当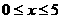 时,y的最小值为 .
时,y的最小值为 .
6.(10南通市) 设x1、x2 是一元二次方程x2+4x-3=0的两个根,2x1(x22+5x2-3)+a =2,则a=
7.(2010年镇江市)已知实数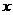 ,
,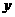 满足
满足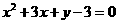 ,
, _______.
_______.
8.(08年内江市)有甲,乙,丙三种商品,如果购甲3件,乙2件,丙1件共需315元钱,购甲1件,乙2件,丙3件共需285元钱,那么购甲,乙,丙三种商品各一件共需_____钱
9.(08年湖北)已知不等式组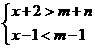 的解集为
的解集为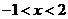 ,则
,则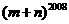 = .
= .
10.(08梅州)已知直线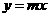 与双曲线
与双曲线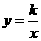 的一个交点A的坐标为
的一个交点A的坐标为 ,则
,则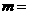 ,
,
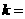 ,它们的另一个交点坐标是
。
,它们的另一个交点坐标是
。
(一)、选择题
1、(08年福州市)已知抛物线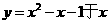 轴的一个点为(m,0)则代数式
轴的一个点为(m,0)则代数式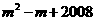 的值为( )
的值为( )
A、2006 B、2007 C、2008 D、2009
2.(10枣庄市)如图,数轴上A、B两点表示的数分别为-1和,点B关于点A的对称点为C,则点C所表示的数为( )
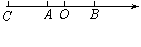 A.―2―
B.―1―
A.―2―
B.―1―
 C.―2+
D.1+
C.―2+
D.1+
3.(10枣庄市)如图,正△AOB的顶点A在反比例函数
y=(x>0)的图象上,则点B的坐标为( )
A.(2,0) B.(,0) C.(2,0) D.(,0)
4.(10岳阳市)如图,⊙O的圆心在定角∠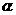 (0°<
(0°<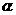 <180°)的角平分线上运动,且⊙O与∠
<180°)的角平分线上运动,且⊙O与∠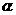 的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图像大致是( )
的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图像大致是( )

[复习要点]
初中代数综合题的特点:代数综合题是初中数学中知识覆盖面最广,综合性最强,解题方法灵活、多样的题型之一.近几年的中考综合题多以代数知识为主.解代数综合题必须认真审题、正确分析理解题意.解题过程中常用到转化、数形结合、分类讨论、方程等数学思想与方法.
[例题解析]
例1: 某化工原料经销公司购进7O00 kg某种化工原料,购进价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于每千克30元,市场调查发现:单价定为每千克70元时,日均销售60kg;单价每降低l元时,均多售出2kg.在销售过程中,每天还要支出其他费用500元(天数不足一天时。按一天计算).设销售单价为 x元,日均获利为y元.
(1)求y关于 x的函数关系式及 的取值范围;
(2)用(1)中求得的函数关系式 指出单价定为多少元时日均获利最多?为多少元?
(3)若将这种化工原料全部售出。比较|{均获利最多和销售单价最高这两种销售方式,哪一种获总利较多?多多少?
解析:此题要抓住“日均获利=每千克获利×销售量-每天支出”这个数量关系。
(1)因为销售单价为x 元,则每千克降低(70一x )元,日均多售2(70--x)kg,日均销量[60+2(70-x)] kg , 每千克获利(x 一30)元,依题意得y=(x 一30) [60+2(70一x)]一500,即为y=(x -30) (200 -2x) -500= -2x2+260x-6500 (30~x≤7O). ①
(2)由式①得Y=一2(x 一65)+1 950.故单价为65元时,日均获利最多为1950元.
(3)当日均获利最多时,单价为65元,日均销售60+2(70一65)=70(kg)。总利润为1 950× 1 00=195 000(元).当销售单价最高为70元时,日均销售为60kg,销售l l7天,获总利为(70-30)×7 000-117×500=221 500(元) , 221 500 -195 000=26 500(元).所以,销售单价最高时获总利较多,多获利26 500元.
反思:解数学应用题的主要思路是构建数学模型,建立函数关系,再利用函数的特征来求解.
例2 、(2009湖州市)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加。据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆。
(1)若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位。据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案。
解析:(1)设家庭轿车拥有量的年平均增长率为x,根据题意,得64(1+x)2=100。解得
x=1/4=25%或x=-9/4(不符合题意,舍去)。则100×(1+25%)=125。即该小区到2009年底家庭轿车将达到125辆。
(2)设该小区可建室内车位a个,则可建露天车位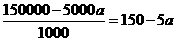 ,可得:
,可得: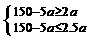 解得
解得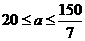 。又a是正整数,所以a=20或21;当a=20时,b=50;当a=21时,b=45。故共有两个方案:方案一,建室内车位20个,露天车位50个;方案二,建室内车位21个,露天车位45个。
。又a是正整数,所以a=20或21;当a=20时,b=50;当a=21时,b=45。故共有两个方案:方案一,建室内车位20个,露天车位50个;方案二,建室内车位21个,露天车位45个。
反思:此题需结合方程(组)、不等式(组)进行解答,综合程度较高,有一定的难度。
[实弹射击]
10、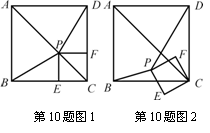 如图(1),已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
如图(1),已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1) 求证:BP=DP;
(2) 如图47(2),若四边形PECF绕点C旋转,在旋转过程中是否总有BP=DP?若是,请证明之;若不是,请举出反例;
(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在旋转的过程中长度始终相等,并证明之.
9、如图,四边形ABCD中,AC=6,BD=8且AC⊥BD顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
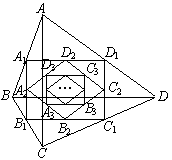 (1)证明:四边形A1B1C1D1是矩形;
(1)证明:四边形A1B1C1D1是矩形;
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积;
(3)求四边形A5B5C5D5的周长.
8、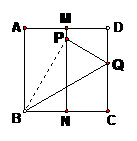 如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PQ.
如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PQ.
(1)求MP的长度; ⑵求证:以PQ为边长的正方形的面积等于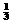 .
.
7、等腰梯形ABCD中,AB=15,AD=20,∠C=30º. M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.
(1)设ND为x,用x表示出点N到AB的距离,并写出x的取值范围.
(2)设t=10-x,用t表示△AMN的面积.
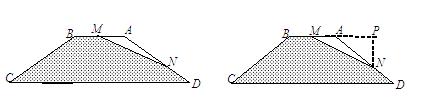 (3)求△AMN的面积的最大值,并判断取最大值时△AMN的形状.
(3)求△AMN的面积的最大值,并判断取最大值时△AMN的形状.
6、如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3)。点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动。当这两点中有一点到达自己的终点时,另一点也停止运动。
(1)设从出发起运动了x秒,且x﹥2.5时,Q点的坐标;
(2)当x等于多少时,四边形OPQC为平行四边形?
(3)四边形OPQC能否成为等腰梯形?说明理由。
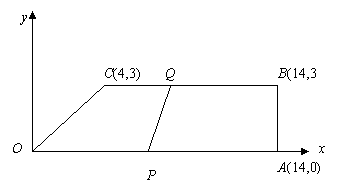 (4)设四边形OPQC的面积为y,求出当 x﹥2.5时y与x的函数关系式;并求出y的最大值;
(4)设四边形OPQC的面积为y,求出当 x﹥2.5时y与x的函数关系式;并求出y的最大值;
5、 如图,梯形ABCD中,AD∥BC,M、N、P、Q分别为AD、BC、BD、AC的中点。求证:MN和PQ互相平分。
如图,梯形ABCD中,AD∥BC,M、N、P、Q分别为AD、BC、BD、AC的中点。求证:MN和PQ互相平分。
4、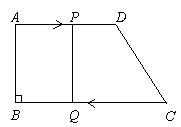 如图,梯形ABCD中,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1m/s的速度移动,点Q从C点开始沿CB边向B以2m/s的速度移动,如果P、Q分别从A、C同时出发,设移动时间为t秒,求:
如图,梯形ABCD中,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1m/s的速度移动,点Q从C点开始沿CB边向B以2m/s的速度移动,如果P、Q分别从A、C同时出发,设移动时间为t秒,求:
(1)t为何时,四边形ABQP为矩形?
(2)t为何时,四边形PQCD为等腰梯形?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com