
题目列表(包括答案和解析)
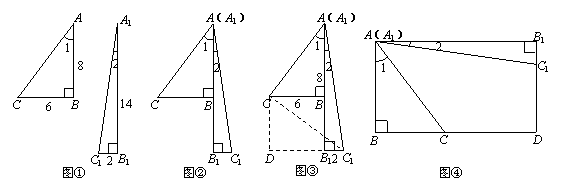
26.(10分)小许在动手操作时,发现直角边长分别为6,8和直角边长分别为2,14的两个直角三角形中(如图①),∠1和∠2可以拼成一个45°的角(如图②),但他不会说理,于是找来几个同学一起研究这个问题.
(1)甲同学发现,只要在图③中连接CC1,过C作CD⊥B1C1,交C1B1的延长线于点D并能计算出CC1的长度,就可以说明△ACC1是等腰直角三角形,从而说明∠1+∠2=45°,请写出甲同学的说理过程;
(2)乙同学发现,只要两个直角三角形的直角边长分别为a,b和直角边长分别为a+b,a-b(a>b),利用两个直角三角形构造出的矩形(如图④),同样可以说明∠1+∠2=45°,请写出乙同学的说理过程;
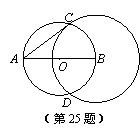
25.(10分)如图,AB是⊙O的直径,AB=10,以B为圆心画圆.
(1)若⊙B和⊙O相交,设交点为 C、D;
①试判断直线AC与⊙B的关系,并说明理由;
②若⊙B的半径是6,连接CO、OD、DB、BC,求四边形CODB的面积;
(2)若⊙B与⊙O相切,则⊙B的半径= ▲ .
24.(8分)如图,是设计师为小许家厨房的装修给出的俯视图,尺寸如图所示,DF边上有一个80 cm宽的门,留下墙DE长为200cm.冰箱摆放在图纸中的位置,冰箱的俯视图是一个边长为60 cm的正方形,为了利于冰箱的散热,厂家建议冰箱的后面和侧面都至少留有10 cm的空隙,为了方便使用,建议冰箱的门至少要能打开到120°(图中∠ABC=120°).
(1)为了满足厂家的建议,图纸中的冰箱离墙DE至少多少厘米?
(2)为了满足厂家建议的散热留空的最小值,小许想拆掉部分墙DE,将门扩大,同时又满足厂家建议的开门角度,那么至少拆掉多少厘米的墙,才能满足上述要求?(结果精确到0.1cm)(参考数据:≈1.41,≈1.73).

23.(8分)将水平相当的A、B、C、D四人随机平均分成甲、乙两组进行乒乓球单打比赛,每组的胜者进入下一轮决赛.
(1)A、B被分在同一组的概率是多少?
(2)A、B在下一轮决赛中相遇的概率是多少?
22.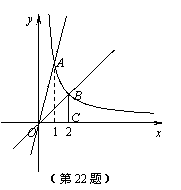 (8分)如图,反比例函数y1=(x>0)与正比例函数y2=mx和y3=nx分别交于A,B两点.已知A、B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.
(8分)如图,反比例函数y1=(x>0)与正比例函数y2=mx和y3=nx分别交于A,B两点.已知A、B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.
(1)当y2>y1时,x的取值范围是 ▲ ;
(2)求出y1和y3的关系式;
(3)直接写出不等式组的解集 ▲ .
21.(6分)表①是2005年日本爱知世博会和2007年西班牙萨拉戈萨世博会文化演艺活动基本数据统计表,图①是爱知世博会各类活动场次统计,图②是萨拉戈萨世博会各类活动场次统计.(数据来自于世博会官网)
|
|
会期(天) |
活动数(千场) |
日均活动(场) |
|
2005年爱知 |
185 |
11 |
59 |
|
2007年萨拉戈萨 |
93 |
5 |
▲ |
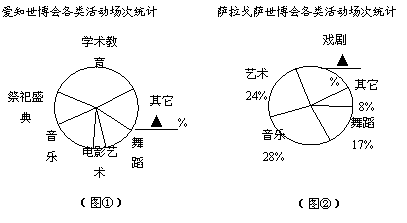
(1) 完成表①中的数据(结果保留整数),完成图①、图②中的空格;
(2) 两届世博会中哪一届音乐类演艺活动的场次多?
20.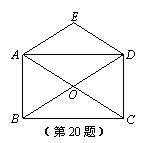 (8分)已知:如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,DE∥AC,AE∥BD.
(8分)已知:如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,DE∥AC,AE∥BD.
求证:(1)四边形ABCD是矩形;
(2)四边形AODE是菱形.
19.(8分)
(1)(4分)解不等式组并写出它的所有整数解.
(2)(4分)化简(-)÷.
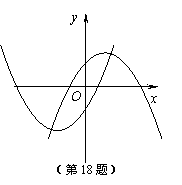
18.函数y1=-ax2+ax+1,y2= ax2+ax-1(其中a为常数,且a>0)的图像如图所示,请写出一条与上述两条抛物线有关的不同类型的结论 ▲ .
17. 菱形边长为6,一个内角为60°,顺次连接这个菱形各边中点所得的四边形周长为 ▲
.
菱形边长为6,一个内角为60°,顺次连接这个菱形各边中点所得的四边形周长为 ▲
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com