
题目列表(包括答案和解析)
8.计算: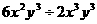 = .
= .
[请将结果直接填入答题纸的相应位置上.]
- 1 -
7.求值: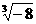 = .
= .
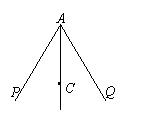
6.如图三,已知AC平分∠PAQ,点B、D分别在边AP、AQ上.
如果添加一个条件后可推出AB=AD,那么该条件不可以是
A.BD⊥AC B.BC=DC
C.∠ACB=∠ACD D.∠ABC=∠ADC
5.下列命题中正确的是
A.对角线互相垂直且相等的四边形是正方形
B.如果一条直线上有两点到另一条直线上的距离相等,那么这两条直线互相平行
C.如果半径分别为3和1的两圆相切,那么两圆的圆心距一定是4
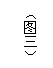
 D.有一个内角是
D.有一个内角是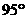 的两个等腰三角形相似
的两个等腰三角形相似
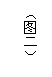
4.如图二,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰
为半圆。当水面上涨1米时,桥孔中的水面宽度A’B’为
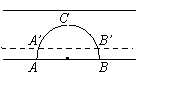 A.
A.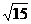 米
B.
米
B.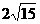 米
米
C.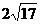 米
D.不能计算
米
D.不能计算
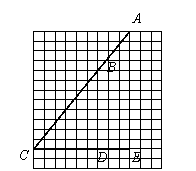
3.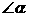 在正方形网格中的位置如图一所示,那么
在正方形网格中的位置如图一所示,那么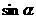 应用哪些
应用哪些
点联结成的线段的比值表示
A.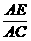 B.
B.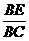 C.
C.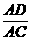 D.
D.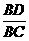
2.解方程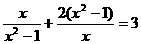 时,设
时,设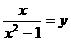 ,则原方程化为y的整式方程为
,则原方程化为y的整式方程为
A.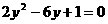 B.
B.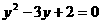
 C.
C.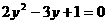 D.
D.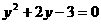
[下列各题的四个结论中,有且只有一个选项是正确的。选择正确项的代号并填涂在答题纸的相应位置上.]
1.下列各实数中,属有理数的是
A.π
B.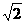 C.
C.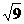 D.cos45°
D.cos45°
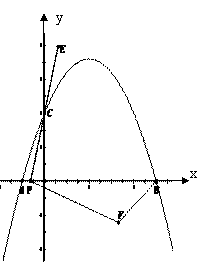
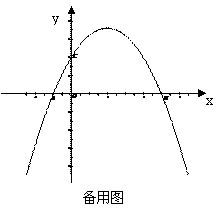
26.(10分)如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(-1,0),(5,0),(0,2).
(1)求过A、B、C三点的抛物线解析式.
(2)若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P运动的时间为t秒,(0≤t≤6)设△PBF的面积为S.
①求S与t的函数关系式.
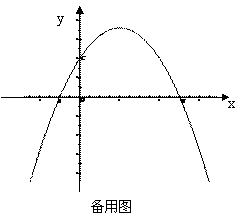
②当t是多少时,△PBF的面积最大,最大面积是多少?
 (3)点P在移动的过程中,△PBF能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.
(3)点P在移动的过程中,△PBF能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.

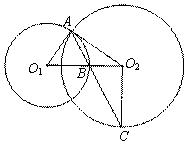
25.(7分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;(2)证明:AB·BC=2O2B·BO1;(3)如果AB·BC=12,O2C=4,求AO1的长.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com