
题目列表(包括答案和解析)
1.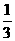
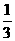 -3的绝对值是
-3的绝对值是
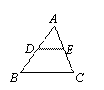 A.3
B.-3
C.-
D.
A.3
B.-3
C.-
D.
30.(D) 8
(D) 某鞋店有甲、乙两款鞋各30双,甲鞋一双200元,乙鞋一双50元。该店促销的方式:买一双甲鞋,送一双乙鞋;只买乙鞋没有任何优惠。若打烊后得知,此两款鞋共卖得1800元,还剩甲鞋x双、乙鞋y双,则依题意可列出下列哪一个方程式?
(A) (B)
(B)
(C) (D)
(D)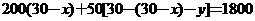
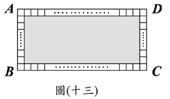 (D)31. 如图(十三),将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形。根据右图,若灰色长方形之长与宽的比为5:3,则
(D)31. 如图(十三),将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形。根据右图,若灰色长方形之长与宽的比为5:3,则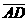 :
: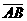 =?
=?
(A) 5:3 (B) 7:5
(C) 23:14 (D) 47:29
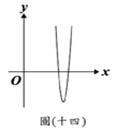 (A)32. 如图(十四),将二次函数
(A)32. 如图(十四),将二次函数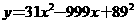 的图形画在坐标平面上,判断方程式
的图形画在坐标平面上,判断方程式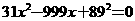 的两根,下列叙述何者正确?
的两根,下列叙述何者正确?
(A)两根相异,且均为正根
(B)两根相异,且只有一个正根
(C)两根相同,且为正根
(D)两根相同,且为负根
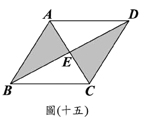 (D)33. 图(十五)为一个四边形
(D)33. 图(十五)为一个四边形 ,其中
,其中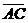 与
与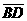 交于E点,且两灰色区域的面积相等。若
交于E点,且两灰色区域的面积相等。若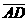 =11,
=11,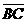 =10,则下列关系何者正确?
=10,则下列关系何者正确?
(A)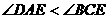
(B)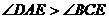
(C)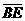 >
>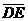
(D)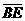 <
<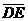
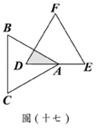
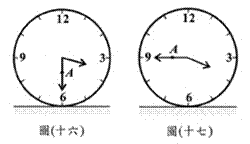 (D)34. 图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分?
(D)34. 图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分?
(A)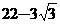 (B)
(B)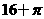 (C)18(D)19
(C)18(D)19
18.(D) 10
(A) 解不等式1-2x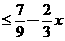 ,得其解的范围为何?
,得其解的范围为何?
(A)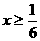 (B)
(B)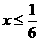 (C)
(C)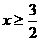 (D)
(D)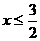
(C)19. 若a、b两数满足a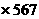 3=103,a
3=103,a 103=b,则
103=b,则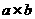 之值为何?
之值为何?
(A)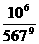 (B)
(B)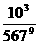 (C)
(C)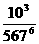 (D)
(D)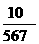
(B)20. 若一元二次方程式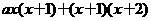
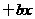
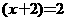 的两根为0、2,则
的两根为0、2,则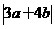 之值为何?(A) 2 (B) 5 (C) 7 (D) 8
之值为何?(A) 2 (B) 5 (C) 7 (D) 8
(A)21. 坐标平面上有一个线对称图形,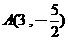 、
、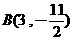 两点在此图形上且互为对称点。若此图形上有一点
两点在此图形上且互为对称点。若此图形上有一点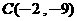 ,则C的对称点坐标为何?
,则C的对称点坐标为何?
(A)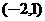 (B)
(B)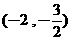 (C)
(C)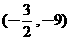 (D)
(D)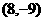
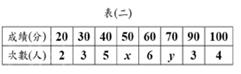 (B)22. 表(二)为某班成绩的次数分配表。已知全班共有38人,且众数为50分,中位数为60分,求
(B)22. 表(二)为某班成绩的次数分配表。已知全班共有38人,且众数为50分,中位数为60分,求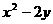 之值为何?
之值为何?
(A) 33 (B) 50 (C) 69 (D) 90
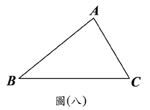 (B)23. 如图(八),三边均不等长的
(B)23. 如图(八),三边均不等长的 ,若在此三角形内找一点O,使得
,若在此三角形内找一点O,使得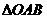 、
、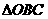 、
、 的面积均相等。判断下列作法何者正确?
的面积均相等。判断下列作法何者正确?
(A) 作中线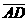 ,再取
,再取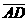 的中点O
的中点O
(B) 分别作中线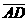 、
、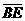 ,再取此两中线的交点O
,再取此两中线的交点O
(C) 分别作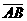 、
、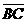 的中垂线,再取此两中垂线的交点O
的中垂线,再取此两中垂线的交点O
(D) 分别作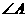 、
、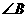 的角平分线,再取此两角平分线的交点O
的角平分线,再取此两角平分线的交点O
(C)24. 下列四个多项式,哪一个是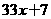 的倍式?
的倍式?
(A)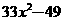 (B)
(B)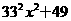 (C)
(C)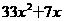 (D)
(D)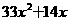
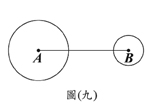 (B)25. 如图(九),圆A、圆B的半径分别为4、2,且
(B)25. 如图(九),圆A、圆B的半径分别为4、2,且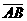 =12。若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长?
=12。若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长?
(A) 3 (B) 4
 (C)
5 (D) 6
(C)
5 (D) 6
(D)26. 图(十)为一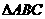 ,其中D、E两点分别在
,其中D、E两点分别在 、
、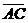 上,且
上,且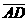 =31,
=31,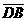 =29,
=29,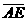 =30,
=30,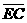 =32。若
=32。若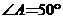 ,则图中
,则图中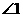 、
、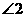 、
、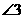 、
、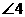 的大小关系,下列何者正确?
的大小关系,下列何者正确?
(A)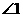 >
>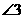
(B)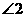 =
=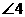
(C)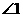 >
>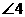
(D)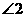 =
=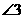
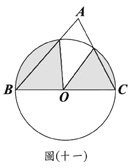 (D)27. 图(十一)为
(D)27. 图(十一)为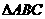 与圆O的重迭情形,其中
与圆O的重迭情形,其中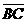 为圆O之直径。若
为圆O之直径。若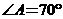 ,
,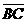 =2,则图中灰色区域的面积为何?
=2,则图中灰色区域的面积为何?
(A)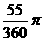 (B)
(B)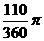
(C)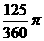 (D)
(D)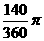
(B)28. 某直角柱的两底面为全等的梯形,其四个侧面的面积依序为20平方公分、36平方公分、20平方公分、60平方公分,且此直角柱的高为4公分。求此直角柱的体积为多少立方公分?
 (A)
136 (B) 192 (C) 240 (D) 544
(A)
136 (B) 192 (C) 240 (D) 544
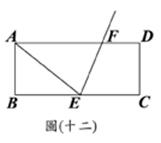
(C)29. 如图(十二),长方形ABCD中,E为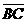 中点,作
中点,作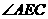 的角平分线交
的角平分线交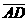 于F点。若
于F点。若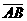 =6,
=6,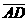 =16,则
=16,则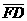 的长度为何?
的长度为何?
(A) 4
(B) 5
(C) 6
31.(D) 75
(A) 關於方程式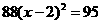 的兩根,下列判斷何者正確?
的兩根,下列判斷何者正確?
(A)一根小於1,另一根大於3
(B)一根小於-2,另一根大於2
(C)兩根都小於0
(D)兩根都大於2
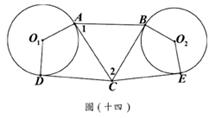 (A)32. 圖(十四)中,
(A)32. 圖(十四)中,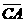 、
、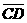 分別切圓O1於A、D兩點,
分別切圓O1於A、D兩點, 、
、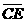 分別切圓O2於B、E兩點。
若∠1=60∘,∠2=65∘,判斷
分別切圓O2於B、E兩點。
若∠1=60∘,∠2=65∘,判斷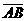 、
、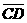 、
、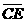 的長度,下列關係何者正確?
的長度,下列關係何者正確?
(A)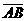 >
>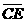 >
>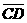
(B)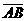 =
=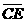 >
>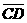
(C)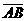 >
>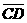 >
>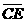
(D)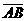 =
=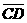 =
=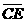

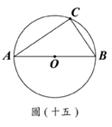 (D)33. 如圖(十五),
(D)33. 如圖(十五),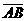 為圓O的直徑,在圓O上取異於A、B的一點C,並連接
為圓O的直徑,在圓O上取異於A、B的一點C,並連接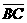 、
、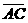 。若想在
。若想在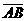 上取一點P,使得P與直線BC的距離等於
上取一點P,使得P與直線BC的距離等於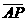 長,判斷下列四個作法何者正確?
長,判斷下列四個作法何者正確?
(A)作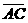 的中垂線,交
的中垂線,交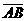 於P點
於P點
(B)作∠ACB的角平分線,交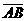 於P點
於P點
(C)作∠ABC的角平分線,交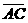 於D點,過D作直線BC的平行線,交
於D點,過D作直線BC的平行線,交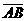 於P點
於P點
(D)過A作圓O的切線,交直線BC於D點,作∠ADC的角平分線,交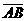 於P點
於P點
(C)34. 如圖(十六),有兩全等的正三角形ABC、DEF,且D、A分別為△ABC、△DEF的重心。固定D點,將△DEF逆時針旋轉,使得A落在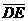 上,如圖(十七)所示。求圖(十六)與圖(十七)中,兩個三角形重疊區域的面積比為何?
上,如圖(十七)所示。求圖(十六)與圖(十七)中,兩個三角形重疊區域的面積比為何?
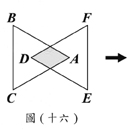
(A) 2:1
(B) 3:2
(C) 4:3
(D) 5:4
試題結束
25.(D) 70
(B) 若有兩圓相交於兩點,且圓心距離為13公分,則下列哪一選項中的長度可能為此兩圓的半徑?
(A) 25公分、40公分
(B) 20公分、30公分
(C) 1公分、10公分
(D) 5公分、7公分
(B)26. 如圖(七),將某四邊形紙片ABCD的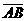 向
向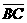 方向摺過去(其中
方向摺過去(其中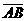 <
<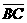 ),使得A點落在
),使得A點落在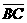 上,展開後出現摺線
上,展開後出現摺線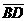 ,如圖(八)。將B點摺向D,使得B、D兩點重疊,如圖(九),展開後出現摺線
,如圖(八)。將B點摺向D,使得B、D兩點重疊,如圖(九),展開後出現摺線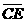 ,如圖(十)。根據圖(十),判斷下列關係何者正確?
,如圖(十)。根據圖(十),判斷下列關係何者正確?
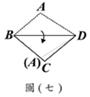
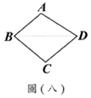
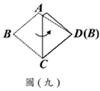
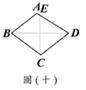
(A) 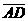 //
//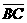
(B) 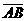 //
//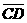
(C)∠ADB=∠BDC
(D)∠ADB>∠BDC
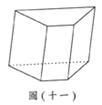 (C)27. 圖(十一)為一直角柱,其中兩底面為全等的梯形,其面積和為16;四個側面均為長方形,其面積和為45。若此直角柱的體積為24,則所有邊的長度和為何?
(C)27. 圖(十一)為一直角柱,其中兩底面為全等的梯形,其面積和為16;四個側面均為長方形,其面積和為45。若此直角柱的體積為24,則所有邊的長度和為何?
(A) 30
(B) 36
(C) 42
(D) 48
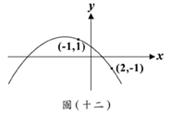 (D)28. 圖(十二)為座標平面上二次函數
(D)28. 圖(十二)為座標平面上二次函數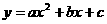 的圖形,且此圖形通
(-1 , 1)、(2 ,-1)兩點。下列關於此二次函數的敘述,何者正確?
的圖形,且此圖形通
(-1 , 1)、(2 ,-1)兩點。下列關於此二次函數的敘述,何者正確?
(A) y的最大值小於0
(B)當x=0時,y的值大於1
(C)當x=1時,y的值大於1
(D)當x=3時,y的值小於0
(C)29. 已知小龍、阿虎兩人均在同一地點,若小龍向北直走160公尺,再向東直走80公尺後,可到神仙百貨,則阿虎向西直走多少公尺後,他與神仙百貨的距離為340公尺?
(A) 100
(B) 180
(C) 220
(D) 260
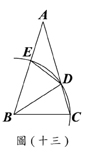 (C)30. 如圖(十三),ΔABC中,以B為圓心,
(C)30. 如圖(十三),ΔABC中,以B為圓心,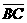 長為半徑畫弧,分別交
長為半徑畫弧,分別交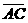 、
、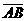 於D、E兩點,並連接
於D、E兩點,並連接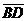 、
、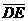 。若∠A=30∘,
。若∠A=30∘,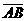 =
=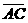 ,則∠BDE的度數為何?
,則∠BDE的度數為何?
(A) 45
(B) 52.5
(C) 67.5
22.(D) 23
(D) 計算多項式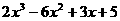 除以(x-2)2後,得餘式為何?
除以(x-2)2後,得餘式為何?
(A) 1
(B) 3
(C) x-1
(D) 3x-3
(B)23. 一籤筒內有四支籤,分別標記號碼1、2、3、4。已知小武以每次取一支且取後不放回的方式,取兩支籤,若每一種結果發生的機會都相同,則這兩支籤的號碼數總和是奇數的機率為何?
(A)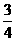
(B)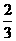
(C)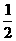
(D)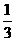
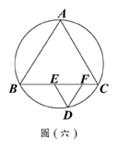 (C)24. 如圖(六),△ABC的外接圓上,AB、BC、CA三弧的度數比為12:13:11。自BC上取一點D,過D分別作直線AC、直線AB的平行線,且交
(C)24. 如圖(六),△ABC的外接圓上,AB、BC、CA三弧的度數比為12:13:11。自BC上取一點D,過D分別作直線AC、直線AB的平行線,且交 於E、F兩點,則∠EDF的度數為何?
於E、F兩點,則∠EDF的度數為何?
(A) 55
(B) 60
(C) 65
21.(D) 14
(A) 表(一)為72人參加某商店舉辦的單手抓糖果活動的統計結果。若抓到糖果數的中位數為a,眾數為b,則a+b之值為何?
 (A) 20
(A) 20
(B) 21
(C) 22
23.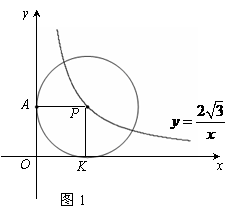 (本题满分12分)
(本题满分12分)
解:(1)∵⊙P分别与两坐标轴相切,
∴ PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴ ∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵OA=OK,
∴四边形OKPA是正方形.……………………2分
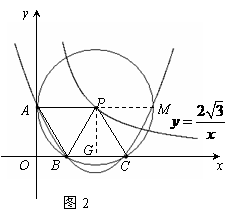 (2)①连接PB,设点P的横坐标为x,则其纵坐标为
(2)①连接PB,设点P的横坐标为x,则其纵坐标为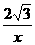 .
.
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC.
∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,
PG=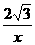 .
.
sin∠PBG=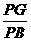 ,即
,即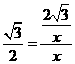 .
.
解之得:x=±2(负值舍去).
∴
PG=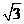 ,PA=BC=2.……………………4分
,PA=BC=2.……………………4分
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴ A(0,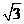 ),B(1,0)
C(3,0).……………………6分
),B(1,0)
C(3,0).……………………6分
设二次函数解析式为:y=ax2+bx+c.
据题意得: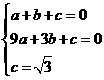
解之得:a=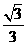 , b=
, b=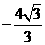 , c=
, c=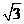 .
.
∴二次函数关系式为: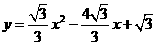 .……………………9分
.……………………9分
②解法一:设直线BP的解析式为:y=ux+v,据题意得:
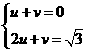
解之得:u=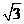 , v=
, v=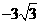 .
.
∴直线BP的解析式为: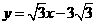 .
.
过点A作直线AM∥PB,则可得直线AM的解析式为: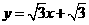 .
.
解方程组: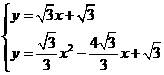
得: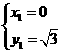 ;
; 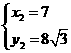 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为: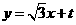 .
.
∴0=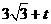 .
.
∴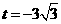 .
.
∴直线CM的解析式为: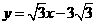 .
.
解方程组: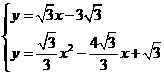
得: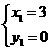 ;
; 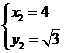 .
.
综上可知,满足条件的M的坐标有四个,
分别为:(0,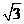 ),(3,0),(4,
),(3,0),(4,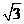 ),(7,
),(7,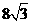 ).…………………12分
).…………………12分
解法二:∵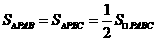 ,
,
∴A(0,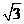 ),C(3,0)显然满足条件.
),C(3,0)显然满足条件.
延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴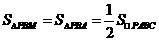 .
.
∴点M的纵坐标为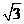 .
.
又点M的横坐标为AM=PA+PM=2+2=4.
∴点M(4,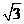 )符合要求.
)符合要求.
点(7,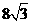 )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0,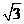 ),(3,0),(4,
),(3,0),(4,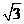 ),(7,
),(7,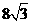 ).…………………12分
).…………………12分
解法三:延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴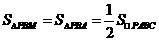 .
.
∴点M的纵坐标为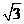 .
.
即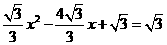 .
.
解得: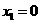 (舍),
(舍),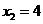 .
.
∴点M的坐标为(4,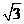 ).
).
点(7,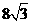 )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0,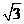 ),(3,0),(4,
),(3,0),(4,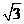 ),(7,
),(7,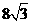 ).…………………12分
).…………………12分
22.(本题满分10分)
●观察计算: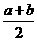 >
>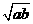 ,
, 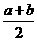 =
=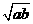 . …………………2分
. …………………2分
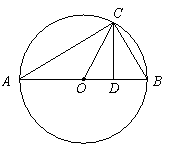 ●探究证明:
●探究证明:
(1)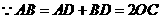 ,
,
∴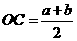 …………………3分
…………………3分
 AB为⊙O直径,
AB为⊙O直径,
∴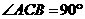 .
.
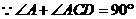 ,
,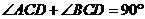 ,
,
∴∠A=∠BCD.
∴△ ∽△
∽△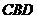 . …………………4分
. …………………4分
∴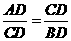 .
.
即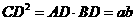 ,
,
∴ .
…………………5分
.
…………………5分
(2)当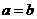 时,
时,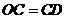 ,
, 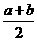 =
=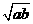 ;
;
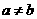 时,
时,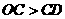 ,
, 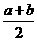 >
>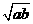 .…………………6分
.…………………6分
●结论归纳: 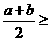
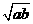 . ………………7分
. ………………7分
●实践应用
设长方形一边长为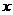 米,则另一边长为
米,则另一边长为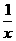 米,设镜框周长为l米,则
米,设镜框周长为l米,则
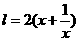 ≥
≥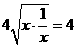 .
……………9分
.
……………9分
当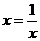 ,即
,即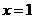 (米)时,镜框周长最小.
(米)时,镜框周长最小.
此时四边形为正方形时,周长最小为4 米. ………………10分
21.(本题满分10分)
解:(1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需(x+25)天.………………………………1分
根据题意得:
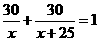 . ………………………………3分
. ………………………………3分
方程两边同乘以x(x+25),得 30(x+25)+30x= x(x+25),
即 x2-35x-750=0.
解之,得x1=50,x2=-15. ………………………………5分
经检验,x1=50,x2=-15都是原方程的解.
但x2=-15不符合题意,应舍去. ………………………………6分
∴ 当x=50时,x+25=75.
答:甲工程队单独完成该工程需50天,则乙工程队单独完成该工程需75天. ……………………7分
(2)此问题只要设计出符合条件的一种方案即可.
方案一:
由甲工程队单独完成.………………………………8分
所需费用为:2500×50=125000(元).………………………………10分
方案二:
甲乙两队合作完成.
所需费用为:(2500+2000)×30=135000(元).……………………10分
其它方案略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com