
题目列表(包括答案和解析)
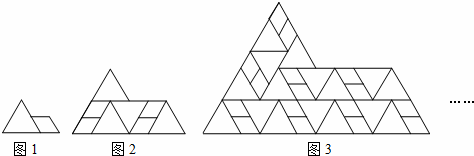
8、(2011•德州)图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),…,则第n个图形的周长是( )
A、2n B、4n
C、2n+1 D、2n+2
考点:规律型:图形的变化类;等边三角形的性质;菱形的性质。
专题:规律型。
分析:从图1到图3,周长分别为4,8,16,由此即可得到通式,利用通式即可求解.
解答:解:下面是各图的周长:
图1中周长为4;
图2周长为8;
图3周长为16;
所以第n个图形周长为2n+1.
故选C.
点评:本题考查了图形的变化规律,首先从图1到图3可得到规律,然后利用规律得到一般结论解决问题.
7、(2011•德州)一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周率”,下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a1,a2,a3,a4,则下列关系中正确的是( )
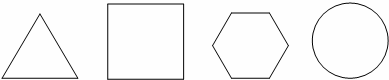
A、a4>a2>a1 B、a4>a3>a2
C、a1>a2>a3 D、a2>a3>a4
考点:正多边形和圆;等边三角形的判定与性质;多边形内角与外角;平行四边形的判定与性质。
专题:计算题。
分析:设等边三角形的边长是a,求出等边三角形的周长,即可求出等边三角形的周率a1;设正方形的边长是x,根据勾股定理求出对角线的长,即可求出周率;设正六边形的边长是b,过F作FQ∥AB交BE于Q,根据等边三角形的性质和平行四边形的性质求出直径,即可求出正六边形的周率a3;求出圆的周长和直径即可求出圆的周率,比较即可得到答案.
解答:解:设等边三角形的边长是a,则等边三角形的周率a1=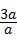 =3
=3
设正方形的边长是x,由勾股定理得:对角线是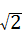 x,则正方形的周率是a2=
x,则正方形的周率是a2=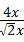 =2
=2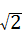 ≈2.828,
≈2.828,
设正六边形的边长是b,过F作FQ∥AB交BE于Q,得到平行四边形ABQF和等边三角形EFQ,直径是b+b=2b,
∴正六边形的周率是a3=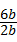 =3,
=3,
圆的周率是a4=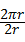 =π,
=π,
∴a4>a3>a2.
故选B.

点评:本题主要考查对正多边形与圆,多边形的内角和定理,平行四边形的性质和判定,等边三角形的性质和判定等知识点的理解和掌握,理解题意并能根据性质进行计算是解此题的关键.
6、(2011•德州)已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如下面右图所示,则函数y=ax+b的图象可能正确的是( )
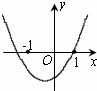
A、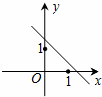 B、
B、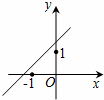
C、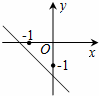 D、
D、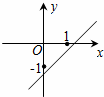
考点:抛物线与x轴的交点;一次函数的图象。
专题:数形结合。
分析:根据图象可得出方程(x﹣a)(x﹣b)=0的两个实数根为a,b,且一正一负,负数的绝对值大,又a>b,则a>0,b<0.根据一次函数y=ax+b的图象的性质即可得出答案.
解答:解:根据图象可得a,b异号,
∵a>b,∴a>0,b<0,
∴函数y=ax+b的图象经过第一、三、四象限,
故选D.
点评:本题考查了抛物线与x轴的交点问题以及一次函数的性质,是重点内容要熟练掌握,
5、(2011•德州)某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
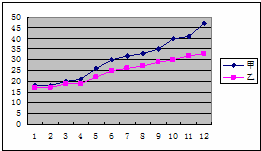
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A、甲运动员得分的极差大于乙运动员得分的极差 B、甲运动员得分的的中位数大于乙运动员得分的的中位数
C、甲运动员的得分平均数大于乙运动员的得分平均数 D、甲运动员的成绩比乙运动员的成绩稳定
考点:方差;折线统计图;算术平均数;中位数;极差。
分析:结合折线统计图,利用数据逐一分析解答即可.
解答:解:A、由图可知甲、乙运动员第一场比赛得分相同,第十二场比赛得分甲运动员比乙运动员得分高,所以甲运动员得分的极差大于乙运动员得分的极差,此选项正确;
B、由图可知甲运动员得分始终大于乙运动员得分,所以甲运动员得分的的中位数大于乙运动员得分的的中位数,此选项正确;
C、由图可知甲运动员得分始终大于乙运动员得分,所以甲运动员的得分平均数大于乙运动员的得分平均数,此选项正确;
D、由图可知甲运动员得分数据波动性较大,乙运动员得分数据波动性较小,乙运动员的成绩比甲运动员的成绩稳定,所以此选项正错误.
故选D.
点评:此题主要结合折线统计图,利用极差、中位数、平均数以及方差来进行分析数据,找到解决问题的突破口.
4、(2011•德州)如图,直线l1∥l2,∠1=40°,∠2=75°,则∠3等于( )
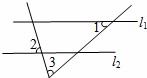
A、55° B、60°
C、65° D、70°
考点:三角形内角和定理;对顶角、邻补角;平行线的性质。
分析:设∠2的对顶角为∠5,∠1在l2上的同位角为∠4,结合已知条件可推出∠1=∠4=40°,∠2=∠5=75°,即可得出∠3的度数
解答:解:∵直线l1∥l2,∠1=40°,∠2=75°,
∴∠1=∠4=40°,∠2=∠5=75°,
∴∠3=65°.
故选C.

点评:本题主要考查三角形的内角和定理,平行线的性质和对顶角的性质,关键在于根据已知条件找到有关相等的角.
3、(2011•德州)温家宝总理强调,“十二五”期间,将新建保障性住房36 000 000套,用于解决中低收入和新参加工作的大学生住房的需求.把36 000 000用科学记数法表示应是( )
A、3.6×107 B、3.6×106
C、36×106 D、0.36×108
考点:科学记数法-表示较大的数。
专题:计算题。
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
解答:解:∵36 000 000=3.6×107;
故选A.
点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2、(2011•德州)一个几何体的主视图、左视图、俯视图完全相同,它一定是( )
A、圆柱 B、圆锥
C、球体 D、长方体
考点:简单几何体的三视图。
专题:应用题。
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解答:解:A、圆柱的主视图、左视图都是长方形,俯视图是圆形;故本选项错误;
B、圆锥的主视图、左视图都是三角形,俯视图是圆形;故本选项错误;
C、球体的主视图、左视图、俯视图都是圆形;故本选项正确;
D、长方体的主视图为长方形、左视图为长方形或正方形、俯视图为长方形或正方形;故本选项错误;
故选C.
点评:本题考查了简单几何体的三视图,锻炼了学生的空间想象能力.
1、(2011•德州)下列计算正确的是( )
A、(﹣8)﹣8=0 B、(﹣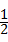 )×(﹣2)=1
)×(﹣2)=1
C、﹣(﹣1)0=1 D、|﹣2|=﹣2
考点:零指数幂;绝对值;有理数的减法;有理数的乘法。
专题:计算题。
分析:利用有理数的减法、有理数的乘法法则和a0=1(a≠0)、负数的绝对值等于它的相反数计算即可.
解答:解:A、(﹣8)﹣8=﹣16,此选项错误;
B、(﹣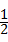 )×(﹣2)=1,此选项正确;
)×(﹣2)=1,此选项正确;
C、﹣(﹣1)0=﹣1,此选项错误;
D、|﹣2|=2,此选项错误.
故选B.
点评:本题考查了有理数的减法、有理数的乘法法则、零指数幂、绝对值的计算.解题的关键是熟练掌握各种运算法则.
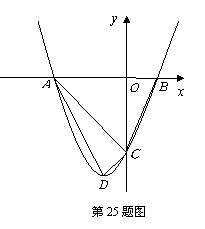
25.(本题满分10分)
如图,在平面直角坐标系 中,把抛物线
中,把抛物线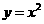 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线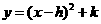 .所得抛物线与
.所得抛物线与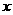 轴交于
轴交于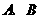 两点(点
两点(点 在点
在点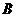 的左边),与
的左边),与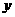 轴交于点
轴交于点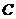 ,顶点为
,顶点为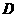 .
.
(1)写出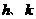 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
 (3)在线段
(3)在线段 上是否存在点
上是否存在点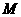 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点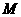 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
绝密☆启用前
24. (本题满分10分)
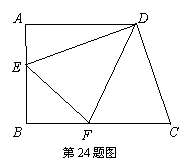 如图,直角梯形ABCD中,AD∥BC,∠A=90°,
如图,直角梯形ABCD中,AD∥BC,∠A=90°,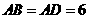 ,
,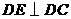 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.
(1)证明: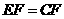 ;
;
(2)当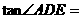
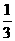 时,求EF的长.
时,求EF的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com