
题目列表(包括答案和解析)
9、(2011•达州)据报道,达州市2010年全年GDP(国内生产总值)约为819.2亿元,请把这个数用科学记数法表示为 8.2×1010元(保留两个有效数字).
考点:科学记数法与有效数字。
专题:探究型。
分析:先根据科学记数法的概念表示出819.2亿元,再保留两个有效数字即可.
解答:解:∵819.2亿元=81920000000元,
∴用科学记数法表示为:8.192×1010元,
∴保留两个有效数字为:8.2×1010.
故答案为:8.2×1010.
点评:本题考查的是科学记数法与有效数字,熟知科学记数法的概念与有效数字的概念是解答此题的关键.
8、(2011•达州)如图所示,在数轴上点A所表示的数x的范围是( )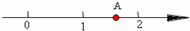
A、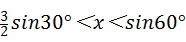 B、
B、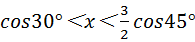
C、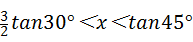 D、
D、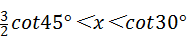
考点:特殊角的三角函数值;实数与数轴。
专题:计算题。
分析:先根据数轴上A点的位置确定出其范围,再根据特殊角的三角函数值对四个选项进行分析即可.
解答:解:由数轴上A点的位置可知,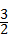 <A<2.
<A<2.
A、由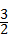 sin30°<x<sin60°可知,
sin30°<x<sin60°可知,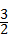 ×
×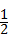 <x<
<x<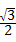 ,即
,即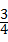 <x<
<x<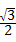 ,故本选项错误;
,故本选项错误;
B、由cos30°<x<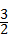 cos45°可知,
cos45°可知,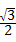 <x<
<x<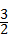 ×
×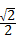 ,即
,即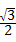 <x<
<x<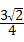 ,故本选项错误;
,故本选项错误;
C、由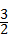 tan30°<x<tan45°可知,
tan30°<x<tan45°可知,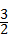 ×
×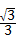 <x<1,即
<x<1,即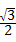 <x<1,故本选项错误;
<x<1,故本选项错误;
D、由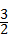 cot45°<x<cot30°可知,
cot45°<x<cot30°可知,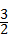 ×1<x<
×1<x<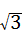 ,即
,即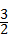 <x<
<x<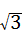 ,故本选项正确.
,故本选项正确.
故选D.
点评:本题考查的是特殊角的三角函数值及在数轴的特点,熟记各特殊角的三角函数值是解答此题的关键.
7、(2008•宁德)如图,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有( )

A、内切、相交 B、外离、相交
C、外切、外离 D、外离、内切
考点:圆与圆的位置关系。
分析:根据圆与圆关系的定义,两个圆与圆没有公共点,并且每个圆上的点都在另一个圆的外部时叫做这两个圆外离;两个圆有两个公共点时叫做这两个圆相交.所以在这个图案中反映出的两圆位置关系有外离和相交.
解答:解:在这个图案中反映出的两圆位置关系有两种外离和相交.故选B.
点评:本题可直接由图案得出圆与圆的位置关系,比较容易.
6、(2011•达州)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为( )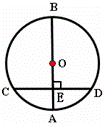
A、5 B、4
C、3 D、2
考点:垂径定理;勾股定理。
专题:计算题。
分析:连接OC,由垂径定理求出CE的长,再根据勾股定理得出线段OE的长.
解答:解:连接OC
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=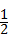 CD,
CD,
∵CD=8,∴CE=4,
∵AB=10,
∴由勾股定理得,OE=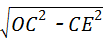 =
=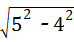 =3.
=3.
故选C.
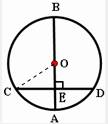
点评:本题考查了垂径定理、勾股定理以及圆中辅助线的做法,是重点知识,要熟练掌握.
5、(2010•攀枝花)如图,在▱ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
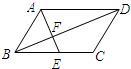
A、S△AFD=2S△EFB B、BF=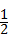 DF
DF
C、四边形AECD是等腰梯形 D、∠AEB=∠ADC
考点:平行四边形的性质;相似三角形的判定与性质。
分析:本题要综合分析,但主要依据都是平行四边形的性质.
解答:解:A、∵AD∥BC
∴△AFD∽△EFB
∴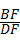 =
=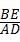 =
=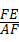 =
=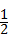
∴S△AFD=2S△ABF,S△ABF=2S△EFB,
故S△AFD=4S△EFB;
B、利用平行四边形的性质可知正确.
C、由∠AEC=∠DCE可知正确.
D、利用等腰三角形和平行的性质即可证明.
故选A.
点评:解决本题的关键是利用相似求得各对应线段的比例关系.
4、(2008•湘潭)已知样本数据1,2,4,3,5,下列说法不正确的是( )
A、平均数是3 B、中位数是4
C、极差是4 D、方差是2
考点:算术平均数;中位数;极差;方差。
专题:计算题。
分析:要求平均数只要求出数据之和再除以总个数即可;根据中位数的定义可求出;对于极差是最大值与最小值的差;方差是样本中各数据与样本平均数的差的平方和的平均数
解答:解:在已知样本数据1,2,4,3,5中,平均数是3;
极差=5﹣1=4;
方差=2.
所以根据中位数的定义,中位数是3,所以B不正确.
故本题选B.
点评:本题考查平均数和中位数.一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.
3、如图是由几个相同的小正方体搭成的一个几何体,它的左视图是( )
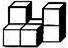
A、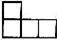 B、
B、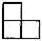
C、 D、
D、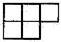
考点:简单组合体的三视图。
分析:根据左视图是从左面看到的图判定则可.
解答:解:左面看去得到的正方形从左往右依次是2,1,故选B.
点评:本题考查了几何体的三视图,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
2、图中所示的几个图形是国际通用的交通标志.其中不是轴对称图形的是( )
A、 B、
B、
C、 D、
D、
考点:轴对称图形。
分析:根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.
解答:解:A、B、D都是轴对称图形,而C不是轴对称图形.
故选C.
点评:本题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
1、(2011•达州)﹣5的相反数是( )
A、﹣5 B、5
C、±5 D、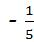
考点:相反数。
专题:计算题。
分析:根据相反数的概念:只有符号不同的两个数是相反数,求解即可.
解答:解:∵|﹣5|=5,且其符号为负号.
∴﹣5的相反数为5.
故选B.
点评:此题主要考查学生对相反数的概念的理解及掌握情况.
25、(12分)如图,已知二次函数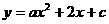
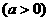 图像的顶点M在反比例函数
图像的顶点M在反比例函数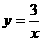 上,且与
上,且与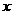 轴交于AB两点。
轴交于AB两点。
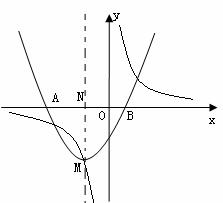 (1)若二次函数的对称轴为
(1)若二次函数的对称轴为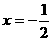 ,试求
,试求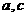 的值;
的值;
(2)在(1)的条件下求AB的长;
(3)若二次函数的对称轴与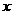 轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com