
题目列表(包括答案和解析)
2.(2010·新创题)定义:离心率e=的椭圆为“黄金椭圆”,已知椭圆E:+=1(a>b>0)的一个焦点为F(c,0)(c>0),P为椭圆E上的任意一点,若a,b,c不是等比数列,则( )
A.E是“黄金椭圆”
B. E一定不是“黄金椭圆”
C. E不一定是“黄金椭圆”
D. 可能不是“黄金椭圆”
解析:假设E为黄金椭圆,则e==,
即c=a,
∴b2=a2-c2=a2-2=a2=ac.
即a,b,c成等比数列,与已知矛盾,故椭圆E一定不是“黄金椭圆”.
答案:B
1.(2010·天门)设P是椭圆+=1上一动点,F1、F2是椭圆的两个焦点,则cos∠F1PF2的最小值是( )
A. B.
C.- D.-
解析:设|PF1|=m,|PF2|=n,由题意m+n=6,
c=,则cos∠F1PF2===-1≥-1=-.
答案:C
13.(2010·南昌调研试题)如图,P是以F1、F2为焦点的双曲线C:-=1上的一点,已知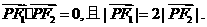
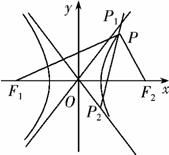
(1)求双曲线的离心率e;
(2)过点P作直线分别与双曲线的两渐近线相交于P1、P2两点,若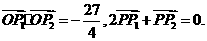 .求双曲线C的方程.
.求双曲线C的方程.
解:(1)利用向量的垂直及双曲线的定义建立等式即可确定,(2)运用向量的坐标运算,利用待定系数法建立方程组即可解得.
(1)由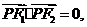 得
得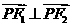 ,即△F1PF2为直角三角形.设
,即△F1PF2为直角三角形.设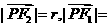 =2r,于是有(2r)2+r2=4c2和2r-r=2a,也就是5×(2a)2=4c2,所以e=.
=2r,于是有(2r)2+r2=4c2和2r-r=2a,也就是5×(2a)2=4c2,所以e=.
(2)==2,可设P1(x1,2x1),P2(x2,-2x2),P(x,y),则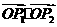 =x1x2-4x1x2=-,
=x1x2-4x1x2=-,
所以x1x2=.①
由2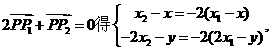 即x=,y=;又因为点P在双曲线-=1上,所以-=1,又b2=4a2,代入上式整理得x1x2=a2②,由①②得a2=2,b2=8,故所求双曲线方程为-=1.
即x=,y=;又因为点P在双曲线-=1上,所以-=1,又b2=4a2,代入上式整理得x1x2=a2②,由①②得a2=2,b2=8,故所求双曲线方程为-=1.
评析:平面向量与平面解析几何的综合考查是近几年高考考查的热点问题,往往通过向量的运算及其几何意义来解决解析几何问题.在解析几何中当直线与曲线相交时,对于交点坐标,若直接求解有时非常复杂,故往往设而不求,即设出点的坐标,利用点在曲线上或其满足的性质求解.本题借助直线与双曲线相交,利用设而不求的思想,结合向量的坐标运算及韦达定理简捷求出.
12.已知曲线C:+x2=1.
(1)由曲线C上任一点E向x轴作垂线,垂足为F,动点P满足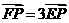 ,求点P的轨迹.P的轨迹可能是圆吗?请说明理由;
,求点P的轨迹.P的轨迹可能是圆吗?请说明理由;
(2)如果直线l的斜率为,且过点M(0,-2),直线l交曲线C于A、B两点,又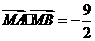 ,求曲线C的方程.
,求曲线C的方程.
解:(1)设E(x0,y0),P(x,y),
则F(x0,0),∵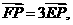 ,
,
∴(x-x0,y)=3(x-x0,y-y0).
∴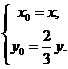
代入+x=1中,得+x2=1为P点的轨迹方程.
当λ=时,轨迹是圆.
(2)由题设知直线l的方程为y=x-2,
设A(x1,y1),B(x2,y2),
联立方程组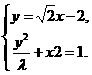
消去y得:(λ+2)x2-4x+4-λ=0.
∵方程组有两解,∴λ+2≠0且Δ>0,
∴λ>2或λ<0且λ≠-2,x1·x2=,
而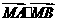 =x1x2+(y1+2)·(y2+2)=x1x2+x1·x2=3x1x2=,
=x1x2+(y1+2)·(y2+2)=x1x2+x1·x2=3x1x2=,
∴=-,解得λ=-14.
∴曲线C的方程是x2-=1.
11.如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=,且△PF1F2的面积为2,又双曲线的离心率为2,求该双曲线的方程.
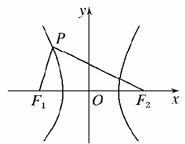
解:设双曲线方程为:-=1(a>0,b>0).
F1(-c,0),F2(c,0),P(x0,y0).
在△PF1F2中,由余弦定理,得:
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos=(|PF1|-|PF2|)2+|PF1|·|PF2|.
即4c2=4a2+|PF1|·|PF2|.
又∵S△PF1F2=2.
∴|PF1|·|PF2|·sin=2.
∴|PF1|·|PF2|=8.
∴4c2=4a2+8,即b2=2.
又∵e==2,∴a2=.
∴双曲线的方程为:-=1.
10.设F1和F2为双曲线-y2=1的两个焦点,点P在双曲线上且满足∠F1PF2=60°,则△F1PF2的面积是______.
解析:在△F1PF2中,由余弦定理,得
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|·cos60°,
∴|F1F2|2=(|PF1|-|PF2|)2+|PF1||PF2|.
又|F1F2|2=20,||PF1|-|PF2||=4.
∴|PF1||PF2|=4,
∴S△F1PF2=|PF1||PF2|sin60°=.
答案:
9.以双曲线的实轴为虚轴,虚轴为实轴的双曲线叫做原双曲线的共轭双曲线,若一条双曲线与它的共轭双曲线的离心率分别为e1,e2,则当它们的实、虚轴都在变化时,e+e的最小值是________.
解析:∵e=,e=,
∴e+e=+
=2++≥2+2
=4(当且仅当a=b时等号成立).
答案:4
8.已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1(-c,0)、F2(c,0).若双曲线上存在点P,使=,则该双曲线的离心率的取值范围是________.
解析:∵e===
==1+,
∵|PF2|>c-a,即e<1+,
∴e2-2e-1<0.
又∵e>1,∴1<e<+1.
答案:(1,+1)
7.已知点P是双曲线-=1上除顶点外的任意一点,F1、F2分别为左、右焦点,c为半焦距,△PF1F2的内切圆与F1F2切于点M,则|F1M|·|F2M|=________.
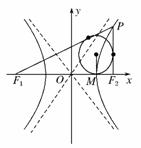
解析:根据从圆外一点向圆所引的两条切线长相等,
|F1M|-|F2M|=|PF1|-|PF2|=2a,
又|F1M|+|F2M|=2c,
解得|F1M|=a+c,|F2M|=c-a,从而|F1M|·|F2M|=c2-a2=b2.
答案:b2
6.已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.[1,2] B.(1,2)
C.[2,+∞) D.(2,+∞)
解析:依题意,应有≥tan60°,又=,
∴≥,解得e≥2.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com