
题目列表(包括答案和解析)
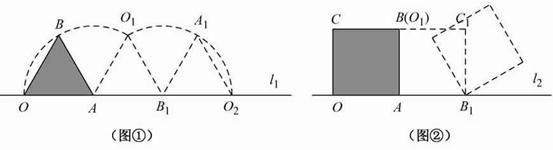
16. (2011江苏苏州,28,9分)(本题满分9分)如图①,小慧同学吧一个正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120°,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2,顶点O所经过的路程是这两段圆弧的长度之和,并且这两端圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°,……,按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片OABC按上述方法经过3次旋转,求顶点O经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形OABC按上述方法经过5次旋转,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是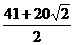 π?
π?
请你解答上述两个问题.
[答案]解问题①:如图,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段弧,即弧OO1、弧O1O2以及弧O2O3,
∴顶点O运动过程中经过的路程为
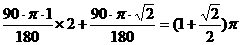 .
.
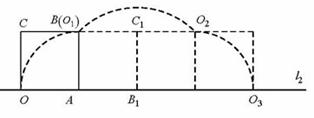
顶点O在此运动过程中所形成的图形与直线l2围成图形的面积为
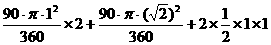 =1+π.
=1+π.
正方形OABC经过5次旋转,顶点O经过的路程为
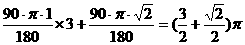 .
.
问题②:∵方形OABC经过4次旋转,顶点O经过的路程为
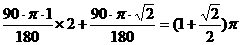
∴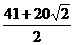 π=20×
π=20×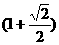 π+
π+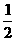 π.
π.
∴正方形纸片OABC经过了81次旋转.
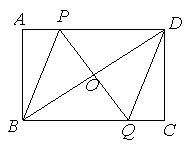
15. (2011广东株洲,23,8分)如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点, PO的延长线交BC于Q.
(1)求证: OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
[答案](1)证明: 四边形ABCD是矩形,
四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,又OB=OD,∠POD=∠QOB,
∴△POD≌△QOB,
∴OP=OQ。
(2)解法一: PD=8-t
∵四边形ABCD是矩形,∴∠A=90°,
∵AD=8cm,AB=6cm,∴BD=10cm,∴OD=5cm.
当四边形PBQD是菱形时, PQ⊥BD,∴∠POD=∠A,又∠ODP=∠ADB,
∴△ODP∽△ADB,
∴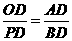 ,即
,即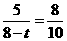 ,
,
解得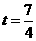 ,即运动时间为
,即运动时间为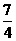 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.
解法二:PD=8-t
当四边形PBQD是菱形时,PB=PD=(8-t)cm,
∵四边形ABCD是矩形,∴∠A=90°,在RT△ABP中,AB=6cm,
∴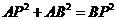 , ∴
, ∴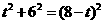 ,
,
解得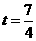 ,即运动时间为
,即运动时间为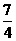 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.
14. (2011甘肃兰州,27,12分)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE。
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由。
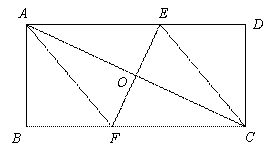

[答案](1)由折叠可知EF⊥AC,AO=CO
∵AD∥BC
∴∠EAO=∠FCO,∠AEO=∠CFO
∴△AOE≌△COF
∴EO=FO
∴四边形AFCE是菱形。
(2)由(1)得AF=AE=10
设AB=a,BF=b,得
a2+b2=100 ①,ab=48 ②
①+2×②得 (a+b)2=196,得a+b=14(另一负值舍去)
∴△ABF的周长为24cm
(3)存在,过点E作AD的垂线交AC于点P,则点P符合题意。
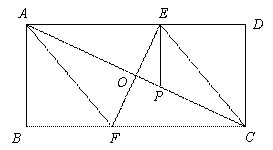

证明:∵∠AEP=∠AOE=90°,∠EAP=∠OAE
∴△AOE∽△AEP
∴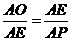 ,得AE2=AO·AP即2AE2=2AO·AP
,得AE2=AO·AP即2AE2=2AO·AP
又AC=2AO
∴2AE2=AC·AP
13. (2011福建泉州,21,9分)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1.
(1)证明:△A1AD1≌△CC1B;
(2)若∠ACB=30°,试问当点C1在线段AC上的什么位置时,四边形ABC1D1是菱形. (直接写出答案)
[答案]
∵矩形ABCD
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1.
∴∠A1=∠DAC,A1D1=AD,AA1=CC1
∴∠A1=∠ACB,A1D1=CB。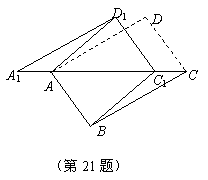

∴△A1AD1≌△CC1B(SAS)。……………6分
当C1在AC中点时四边形ABC1D1是菱形,……………9分
12. (2011浙江省嘉兴,23,12分)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
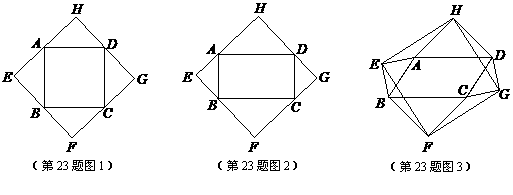
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=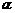 (0°<
(0°<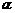 <90°),
<90°),
① 试用含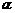 的代数式表示∠HAE;
的代数式表示∠HAE;
② 求证:HE=HG;
③ 四边形EFGH是什么四边形?并说明理由.

[答案](1)四边形EFGH是正方形.
(2) ①∠HAE=90°+a.
在□ABCD中,AB∥CD,∴∠BAD=180°-∠ADC=180°-a;
∵△HAD和△EAB都是等腰直角三角形,∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-a)=90°+a.
②∵△AEB和△DGC都是等腰直角三角形,∴AE=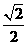 AB,DG=
AB,DG=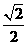 CD,
CD,
在□ABCD中,AB=CD,∴AE=DG,∵△HAD和△GDC都是等腰直角三角形,
∴∠DHA=∠CDG= 45°,∴∠HDG=∠HAD+∠ADC+∠CDG=90°+a=∠HAE.
∵△HAD是等腰直角三角形,∴HA=HD,∴△HAE≌△HDG,∴HE=HG.
③四边形EFGH是正方形.
由②同理可得:GH=GF,FG=FE,∵HE=HG(已证),∴GH=GF=FG=FE,∴四边形EFGH是菱形;∵△HAE≌△HDG(已证),∴∠DHG=∠AHE,又∵∠AHD=∠AHG+∠DHG=90°,∴∠EHG=∠AHG+∠AHE=90°,∴四边形EFGH是正方形.
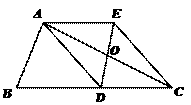
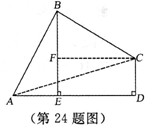
11. (2011浙江衢州,22,10分)如图,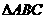 中,
中,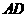 是边
是边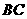 上的中线,过点
上的中线,过点 作
作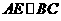 ,过点
,过点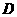 作
作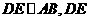 与
与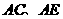 分别交于点
分别交于点 、点
、点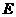 ,连接
,连接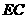
求证: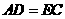 ;
;
当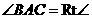 时,求证:四边形
时,求证:四边形 是菱形;
是菱形;
在(2)的条件下,若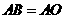 ,求
,求 的值.
的值.
|
[答案].证明:(1)
解法1:因为DE//AB,AE//BC,所以四边形ABDE是平行四边形,
所以AE//BD且AE=BD,又因为AD是边 BC上的中线,所以BD=CD,所以AE平行且等于CD,所以四边形ADCE是平行四边形,所以AD=EC.
BC上的中线,所以BD=CD,所以AE平行且等于CD,所以四边形ADCE是平行四边形,所以AD=EC.
解法2: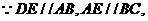
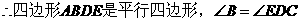
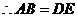
又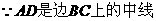
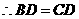
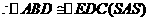
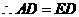
(2)解法1:
证明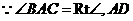 是斜边
是斜边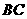 上的中线
上的中线
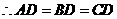
又 四边形
四边形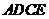 是平行四边形
是平行四边形
 四边形
四边形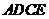 是菱形
是菱形
解法2
证明: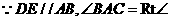
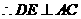
又 四边形
四边形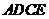 是平行四边形
是平行四边形
 四边形
四边形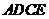 是菱形
是菱形
解法3
证明: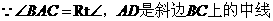
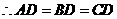
 四边形
四边形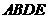 是平行四边形
是平行四边形
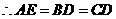
又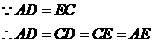
 四边形
四边形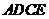 是菱形
是菱形
解法1
解: 四边形
四边形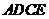 是菱形
是菱形
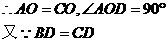
 的中位线,则
的中位线,则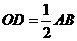
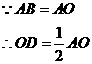
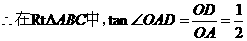
解法2
解: 四边形
四边形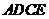 是菱形
是菱形
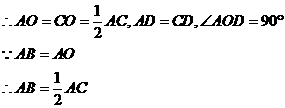
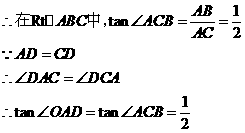
10.(2011宁波市,23,8分)如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AGDB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证四边形DEBF是菱形.
解:(1)□ABCD 中,AB∥CD,AB=CD
∵E、F分别为AB、CD的中点
∴DF=DC,BE=AB
∴DF∥BE,DF=BE
∴四边形DEBF为平行四边形
∴DE∥BF
(2)证明:∵AG∥BD
∴∠G=∠DBC=90°
∴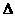 DBC 为直角三角形
DBC 为直角三角形
又∵F为边CD的中点.
∴BF=DC=DF
又∵四边形DEBF为平行四边形
∴四边形DEBF是菱形
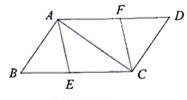
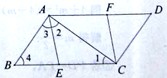
9. (2011 浙江湖州,22,8) 如图已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1) 求证:四边形AECF是平行四边形;
(2) 若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
[答案](1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,
∴AF=EC,∴四边形AECF是平行四边形.
(2)∵四边形AECF是,∴AE=CE,∴∠1=∠2,∵∠BAC=90°,∴∠3=∠90°-∠2,∠4=∠90°-∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=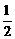 BC=5.
BC=5.
8. (2011山东烟台,24,10分)已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
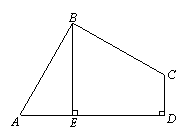 (2)当BE⊥AD于E时,试证明:BE=AE+CD.
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
 [答案](1)证明:连接AC,
[答案](1)证明:连接AC,
∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,∴AB2+BC2=2AB2,
∴AB=BC.
(2)证明:过C作CF⊥BE于F.
∵BE⊥AD,∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,∴△BAE≌△CBF.
∴AE=BF.
∴BE=BF+EF =AE+CD.
7. (2011山东威海,24,11分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
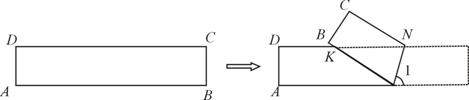
(1)若∠1=70°,求∠MNK的度数.
(2)△MNK的面积能否小于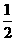 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.

(备用图)
[答案] 解:∵ABCD是矩形,
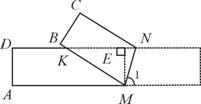 ∴AM∥DN,
∴AM∥DN,
∴∠KNM=∠1.
∵∠KMN=∠1,
∴∠KNM=∠KMN.
∵∠1=70°,
∴∠KNM=∠KMN=70°.
∴∠MNK=40°.
(2)不能.
过M点作ME⊥DN,垂足为点E,则ME=AD=1,
由(1)知∠KNM=∠KMN.
∴MK=NK.
又MK≥ME,
∴NK≥1.
∴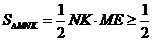 .
.
∴△MNK的面积最小值为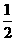 ,不可能小于
,不可能小于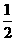 .
.
(3)分两种情况:
情况一:将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=5-x,由勾股定理,得
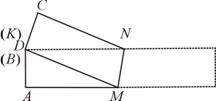
 ,
,
解得,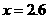 .
.
即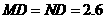 .
.
∴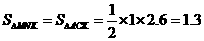 .
(情况一)
.
(情况一)
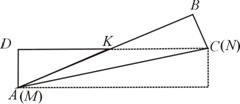 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK=AK= CK=x,则DK=5-x,同理可得
即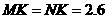 .
.
∴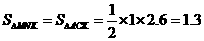 .
.
∴△MNK的面积最大值为1.3. (情况二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com