
题目列表(包括答案和解析)
6、解:(1)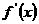 =
=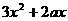
依题意得k=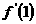 =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
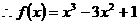 ,把B(1,b)代入得b=
,把B(1,b)代入得b=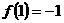
∴a=-3,b=-1
(2)令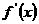 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004。
(1)
已知g(x)=-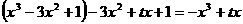
∴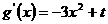
∵0<x≤1,∴-3≤-3x2<0,
①
当t>3时,t-3x2>0,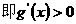
∴g(x)在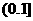 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
②
当0≤t≤3时, 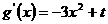
令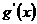 =0,得x=
=0,得x=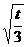
列表如下:
|
x |
(0, 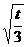 ) ) |
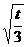 |
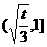 |
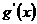 |
+ |
0 |
- |
|
g(x) |
↗ |
极大值 |
↘ |
g(x)在x=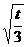 处取最大值-
处取最大值-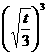 +t
+t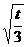 =1
=1
∴t=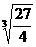 =
=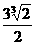 <
<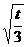 3
3
∴x=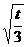 <1
<1
③当t<0时,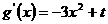 <0,∴g(x)在
<0,∴g(x)在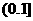 上为减函数,
上为减函数,
∴g(x)在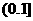 上为增函数,
上为增函数,
∴存在一个a=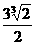 ,使g(x)在
,使g(x)在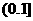 上有最大值1。
上有最大值1。
21.经过抛物线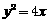 的焦点F的直线
的焦点F的直线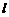 与该抛物线交于
与该抛物线交于 、
、 两点. (12分)
两点. (12分)
(1)若线段 的中点为
的中点为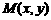 ,直线的斜率为
,直线的斜率为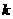 ,试求点
,试求点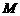 的坐标,并求点
的坐标,并求点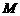 的轨迹方程
的轨迹方程
(2)若直线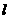 的斜率
的斜率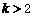 ,且点
,且点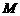 到直线
到直线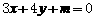 的距离为
的距离为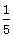 ,试确定
,试确定 的取值范围.
的取值范围.
1(1)解:由题意,可设椭圆的方程为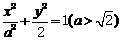 。
。
由已知得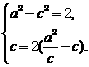 解得
解得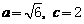
所以椭圆的方程为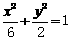 ,离心率
,离心率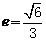 。
。
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为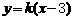 。由方程组
。由方程组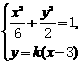
得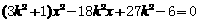 ,依题意
,依题意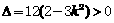 ,得
,得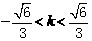 。
。
设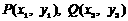 ,则
,则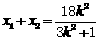 , ①
, ① 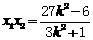 。 ②
。 ②
由直线PQ的方程得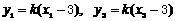 。于是
。于是
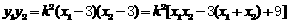 。 ③
。 ③
∵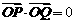 ,∴
,∴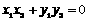 。 ④
。 ④
由①②③④得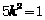 ,从而
,从而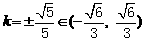 。
。
所以直线PQ的方程为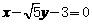 或
或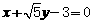
(3,理工类考生做)证明: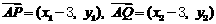 。由已知得方程组
。由已知得方程组
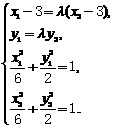
注意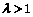 ,解得
,解得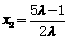
因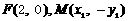 ,故
,故
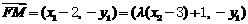
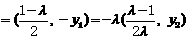 。
。
而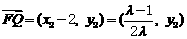 ,所以
,所以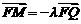 。
。
2 ①f(x)= (2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根
(2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根
3 ①x2=4y ②x1x2=-4 ⑶P(±2,1) SMIN=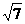
4 .解:因a>1,不防设短轴一端点为B(0,1)
设BC∶y=kx+1(k>0)
则AB∶y=-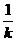 x+1
x+1
把BC方程代入椭圆,
是(1+a2k2)x2+2a2kx=0
∴|BC|=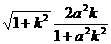 ,同理|AB|=
,同理|AB|=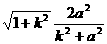
由|AB|=|BC|,得k3-a2k2+ka2-1=0
(k-1)[k2+(1-a2)k+1]=0
∴k=1或k2+(1-a2)k+1=0
当k2+(1-a2)k+1=0时,Δ=(a2-1)2-4
由Δ<0,得1<a<
由Δ=0,得a= ,此时,k=1
,此时,k=1
故,由Δ≤0,即1<a≤ 时有一解
时有一解
由Δ>0即a> 时有三解
时有三解
5 解:依题意,知a、b≠0
∵a>b>c且a+b+c=0
∴a>0且c<0
(Ⅰ)令f(x)=g(x),
得ax2+2bx+c=0.(*)
Δ=4(b2-ac)
∵a>0,c<0,∴ac<0,∴Δ>0
∴f(x)、g(x)相交于相异两点
(Ⅱ)设x1、x2为交点A、B之横坐标
则|A1B1|2=|x1-x2|2,由方程(*),知
|A1B1|2=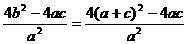
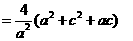
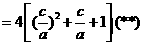
∵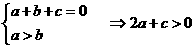 ,而a>0,∴
,而a>0,∴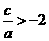
∵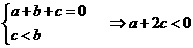 ,∴
,∴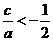
∴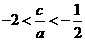
∴4[(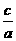 )2+
)2+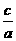 +1]∈(3,12)
+1]∈(3,12)
∴|A1B1|∈( ,2
,2 )
)
30、已知点集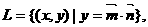 其中
其中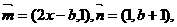 点列
点列 在
在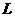 中,
中,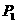 为
为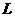 与
与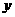 轴的交点,等差数列
轴的交点,等差数列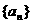 的公差为1,
的公差为1,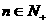 。
。
(1)求数列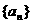 ,
,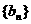 的通项公式;
的通项公式;
(2)若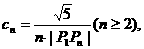 求
求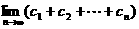 ;
;
(3)若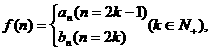 是否存在
是否存在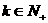 使得
使得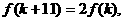 若存在,求出
若存在,求出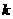 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
28.已知函数f(x)= 的图象过原点,且关于点(-1,1)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}(n∈N*)满足:an>0,a1=1,an+1= [f()]2,求数列{an}的通项公式an,并证明你的结论.
27.(14分)(理)已知椭圆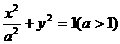 ,直线l过点A(-a,0)和点B(a,ta)
,直线l过点A(-a,0)和点B(a,ta)
(t>0)交椭圆于M.直线MO交椭圆于N.(1)用a,t表示△AMN的面积S;
 (2)若t∈[1,2],a为定值,求S的最大值.
(2)若t∈[1,2],a为定值,求S的最大值.
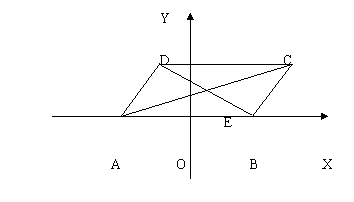
26、已知□ABCD,A(-2,0),B(2,0),且∣AD∣=2
⑴求□ABCD对角线交点E的轨迹方程。
⑵过A作直线交以A、B为焦点的椭圆于M、N两点,且∣MN∣=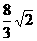 ,MN的中点到Y轴的距离为
,MN的中点到Y轴的距离为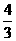 ,求椭圆的方程。
,求椭圆的方程。
⑶与E点轨迹相切的直线l交椭圆于P、Q两点,求∣PQ∣的最大值及此时l的方程。
25、已知抛物线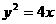 的准线与
的准线与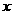 轴交于
轴交于 点,过
点,过 作直线与抛物线交于A、B两点,若线段AB的垂直平分线与X轴交于D(X0,0)
作直线与抛物线交于A、B两点,若线段AB的垂直平分线与X轴交于D(X0,0)
⑴求X0的取值范围。
⑵△ABD能否是正三角形?若能求出X0的值,若不能,说明理由。
24. 已知函数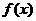 是定义在R上的偶函数.当X
是定义在R上的偶函数.当X 0时,
0时, 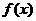 =
=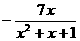 .
.
(I)
求当X<0时, 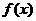 的解析式;
的解析式;
(II)
试确定函数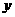 =
=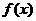 (X
(X 0)在
0)在 的单调性,并证明你的结论.
的单调性,并证明你的结论.
(III)
若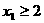 且
且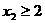 ,证明:|
,证明:|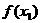 -
-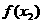 |<2.
|<2.
23、.设函数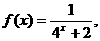
(1)求证:对一切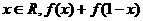 为定值;
为定值;
(2)记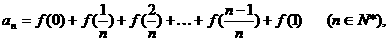 求数列
求数列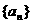 的通项公式及前n项和.
的通项公式及前n项和.
22、直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=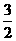 ,BC=
,BC=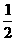 .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.
(1)建立适当坐标系,求椭圆C的方程;
(2)若点E满足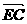

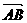 ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且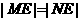 ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com