
题目列表(包括答案和解析)
63、已知f(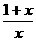 )=
)=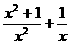 ,则f (x)=( )。
,则f (x)=( )。
(A)(x+1)2 (B)(x-1)2 (C)x2-x+1 (D)x2+x+1
提示:用换元法。
62、如果直线y=ax+2与直线y=3x+b关于直线y=x对称,那么( )。
(A)a=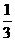 , b=6 (B)a=
, b=6 (B)a=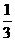 , b=-6 (C)a=3, b=-2 (D)a=3, b=6
, b=-6 (C)a=3, b=-2 (D)a=3, b=6
提示:运用反函数的知识。
61、已知集合Z={θ| cosθ<sinθ, 0≤θ≤2π}, F={θ| tgθ<sinθ},那么Z∩F的区间( )。
(A)(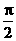 , π) (B)(
, π) (B)(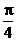 ,
, 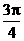 ) (C)(π,
) (C)(π, 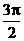 ) (D)(
) (D)(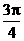 ,
, 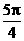 )
)
提示:用图象法解题。
60、如果α, β∈(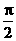 , π),且tgα<ctgβ,那么必有( )。
, π),且tgα<ctgβ,那么必有( )。
(A)α<β (B)β<α
(C)α+β<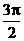 (D)α+β>
(D)α+β>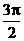
提示:先用诱导公式化成同名函数,再借助函数图象解题。
59、已知等差数列{an}的公差d≠0,且a1, a3,
a9成等比数列,则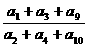 的值是( )。
的值是( )。
(A)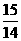 (B)
(B)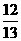 (C)
(C)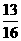 (D)
(D)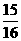
提示:先求a1和公比的关系,再化简。
58、若loga2<logb2<0,则( )。
(A)0<a<b<1 (B)0<b<a<1 (C)a>b>1 (D)b>a>1
提示:先确定对数符号(即真数和底数与1的关系一致时(同时大于或同时小于),为正,不一致时,为负。)再用换底公式。
57、若a, b是任意实数,且a>b,则( )。
(A)a2>b2 (B)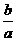 <1 (C)lg(a-b)>0 (D)(
<1 (C)lg(a-b)>0 (D)(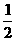 )a<(
)a<(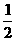 )b
)b
提示:运用平方数、分数、对数、指数函数的概念进行分析。
56、函数y=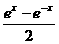 的反函数( )。
的反函数( )。
(A) 是奇函数,它在(0, +∞)上是减函数 (B)是偶函数,它在(0, +∞)上是减函数
(C)是奇函数,它在(0, +∞)上是增函数 (D)是偶函数,它在(0, +∞)上是增函数
提示:先对给出函数进行分析,再运用反函数的概念解题。
55、函数F(x)=(1+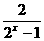 )f (x) (x≠0)是偶函数,且f (x)不恒等于零,则f (x)( )。
)f (x) (x≠0)是偶函数,且f (x)不恒等于零,则f (x)( )。
(A)是奇函数 (B)是偶函数 (C)可能是奇函数,也可能是偶函数 (D)非奇、非偶函数
提示:先讨论y=(1+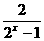 )的奇偶性,再结合题目中的已知内容分析。
)的奇偶性,再结合题目中的已知内容分析。
54、已知直线l1与l2的夹角的平分线为y=x,如果l1的方程是ax+by+c=0(ab>0),那么l2的方程是( )。 (A)bx+ay+c=0 (B)ax-by+c=0 (C)bx+ay-c=0 (D)bx-ay+c=0
提示:联系反函数的概念。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com