
题目列表(包括答案和解析)
1.已知函数y=f(x) (x∈R)满足f(x+3)=f(x+1),且x∈[-1,1]时,f(x)=|x|,则y=f(x)与y=log5x的图象交点的个数是( )
A.3 B.4 C.5 D.6
22.(本小题满分14分)
已知函数f(x-2)=ax2-(a-3)x+a-2(a<0,a∈Z)的图象与x轴有交点.
(1)求a的值;
(2)求f(x)的解析式;
(3)若g(x)=1-[f(x)]2,F(x)=c·g(x)+d·f(x),问是否存在c(c>0),d使得在区间 -(∞,f(2))内是单调递增函数,而在区间(f(2),0)内是单调递减函数?若存在,求c,d之间的关系,并写出推理过程;若不存在,说明理由
20.(本小题满分12分)
学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费用为S元,用电炉烧开水每吨开水费用为P元
S=5x+0.2y+5, P=10.2y+20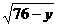
其中x为每吨煤的价格,y为每百度电的价格。如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水。
(1)如果两种方法烧水费用相同,试将每吨煤的价格表示为每百度电价的函数;
(2)如果每百度电价不低于60元,则用煤烧时每吨煤的最高价是多少?
21已知椭圆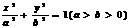 的离心率为
的离心率为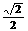 。
。
(1)
若圆(x-2)2+(y-1)2=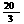 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
(2)
设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600。求 的值。
的值。
18、已知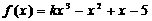 在R上单调递增,记
在R上单调递增,记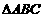 的三内角
的三内角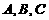 的对应边分别为
的对应边分别为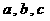 ,若
,若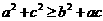 时,不等式
时,不等式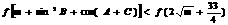 恒成立.
恒成立.
(Ⅰ)求实数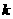 的取值范围;
的取值范围;
(Ⅱ)求角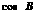 的取值范围;
的取值范围;
(Ⅲ)求实数 的取值范围.
的取值范围.
(19)如图为一几何体的展开图:
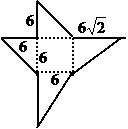
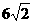
(单位:cm)
(I)沿图中虚线将它们折叠起来,是哪一种特殊几何体?并请画出其直观图,比例尺是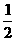 ;
;
(II)需要多少个这样的几何体才能拼成一个棱长为6cm的正方体ABCD-A1B1C1D1,请画出其示意图(需在示意图中分别表示出这种几何体);
(Ⅲ)设正方体ABCD-A1B1C1D1的棱CC1的中点为E,试求:异面直线EB与AB1所成角的余弦值及平面AB1E与平面ABC所成二面角(锐角)的余弦值。
17. 已知集合A={x|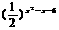 <1},B={x|log4(x+a)<1},若A∩B=
<1},B={x|log4(x+a)<1},若A∩B=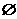 ,求实数a的取值范围.
,求实数a的取值范围.
16、关于函数f(x)=2sin(3x-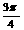 ),有下列命题:①其最小正周期是
),有下列命题:①其最小正周期是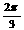 ;②其图象可由y=2sin3x向左平移
;②其图象可由y=2sin3x向左平移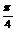 个单位得到;③其表达式可改写为y=2cos(3x-
个单位得到;③其表达式可改写为y=2cos(3x-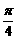 );④在x∈[
);④在x∈[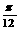 ,
,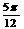 ]上为增函数。
]上为增函数。
其中正确的命题的序号是
15、一块用栅栏围成的长方形土地的长和宽分别为52米和24米,现欲将这块土地内部分割成一些全等的正方形试验田,要求这块土地全部被划分且分割的正方形的边与这块土地的边界平行,现另有2002米栅栏,则最多可将这块土地分割成 块。
14、设圆过双曲线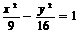 的一个顶点和焦点,圆心在双曲线上,则圆心到双曲线中心的距离
。
的一个顶点和焦点,圆心在双曲线上,则圆心到双曲线中心的距离
。
13、已知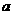 >b,
>b,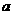 ·b=1则
·b=1则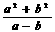 的最小值是
。
的最小值是
。
12、定义在R上的函数y=f(x),在(-∞,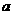 )上是增函数,且函数y=f(x+
)上是增函数,且函数y=f(x+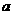 )是偶函数,当x1<
)是偶函数,当x1<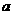 ,x2>
,x2>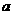 且
且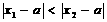 时,有( )
时,有( )
(A) f(2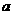 - x1)> f(2
- x1)> f(2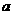 - x2)(B) f(2
- x2)(B) f(2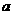 - x1)= f(2
- x1)= f(2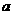 - x2)
- x2)
(C) f(2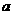 - x1)< f(2
- x1)< f(2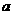 - x2)(D) -f(2
- x2)(D) -f(2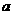 - x1)< f(x2-2
- x1)< f(x2-2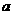 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com