
题目列表(包括答案和解析)
7.(理)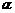 、
、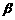 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
(1)a∥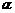 ,b
,b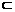
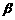 (2)a⊥
(2)a⊥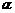 ,b∥
,b∥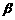 (3)a⊥
(3)a⊥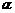 ,b⊥
,b⊥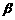
(4)a∥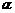 ,b∥
,b∥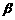 ,且a与
,且a与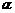 的距离等于b与
的距离等于b与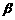 的距离
的距离
A.0个 B.1个 C.2个 D.4个
(文)已知直线l、m、n及平面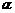 、
、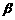 ,下列命题中的假命题是 ( )
,下列命题中的假命题是 ( )
A.若l∥m,m∥n,则l∥n B.若l⊥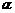 ,n∥
,n∥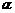 ,则l⊥n
,则l⊥n
C.若l∥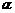 ,n∥
,n∥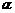 ,则l∥n D.若l⊥
,则l∥n D.若l⊥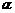 ,
,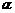 ∥
∥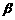 ,则l⊥
,则l⊥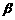
6.已知P是以F1、F2为焦点的椭圆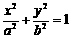 (a > b > 0)上的一点,若
(a > b > 0)上的一点,若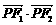 = 0,tan∠PF1F2 =
= 0,tan∠PF1F2 =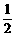 ,则此椭圆的离心率为 ( )
,则此椭圆的离心率为 ( )
A.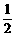 B.
B.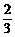 C.
C.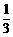 D.
D.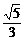
5.设等差数列{an}的前n项和为Sn,且a3 + a5 + a7 = 15,则S9等于 ( )
A.18 B.36 C.45 D.60
4.函数f (x) = 的图像相邻的两条对称轴之间的距离是
( )
的图像相邻的两条对称轴之间的距离是
( )
A.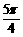 B.5
B.5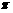 C.
C.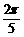 D.
D.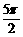
3.函数y = x2 – 1 (x < 0)的反函数是 ( )
A.y =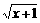 (x < – 1) B.y =
–
(x < – 1) B.y =
–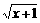 (x < – 1)
(x < – 1)
C.y =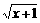 (x > – 1) D.y =
–
(x > – 1) D.y =
–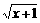 (x > – 1)
(x > – 1)
2.(理)当z =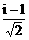 时,z100
+ z50 + 1的值等于
( )
时,z100
+ z50 + 1的值等于
( )
A.1 B.– 1 C.i D.– i
(文)已知全集U = {1,2,3,4,5,6,7},A = {3,4,5},B =
{1,3,6},则A∩( UB)
等于 ( )
UB)
等于 ( )
A.{4,5} B.{2,4,5,7} C.{1,6} D.{3}
1.已知p :不等式| x – 1| + | x + 2 | > m的解集为R,q : f (x) = log5 – 2mx为减函数,则p是q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
24.(江苏卷)已知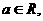 函数
函数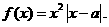
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
解:(1)当a=2时,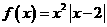 ,则方程f(x)=x即为
,则方程f(x)=x即为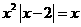
解方程得: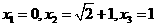
(2)(I)当a>0时,
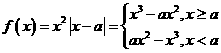 ,
,
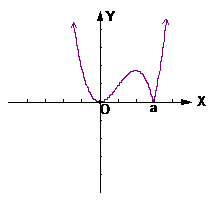
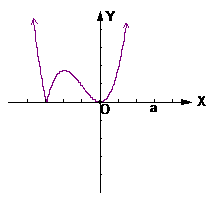
作出其草图见右, 易知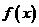 有两个极值点
有两个极值点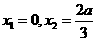 借助于图像可知
借助于图像可知
当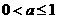 时,函数
时,函数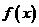 在区间[1,2]上为增函数,此时
在区间[1,2]上为增函数,此时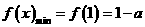
当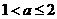 时,显然此时函数的最小值为
时,显然此时函数的最小值为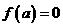
当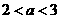 时,
时,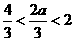 ,此时
,此时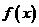 在区间
在区间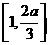 为增函数,在区间
为增函数,在区间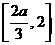 上为减函数,∴
上为减函数,∴ ,又可得
,又可得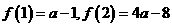
∴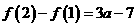
则当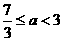 时,
时,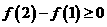 ,此时
,此时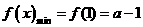
当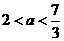 时,
时,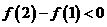 ,此时
,此时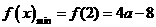
当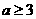 时,
时,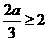 ,此时
,此时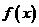 在区间
在区间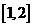 为增函数,故
为增函数,故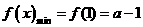
(II)当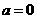 时,
时,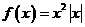 ,此时
,此时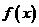 在区间
在区间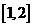 也为增函数,故
也为增函数,故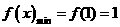
(III)当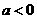 时,其草图见右
时,其草图见右
显然函数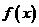 在区间
在区间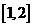 为增函数,故
为增函数,故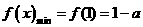
19.(本小题13分)
解: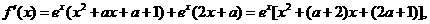
令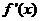 =0得
=0得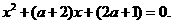
(1)当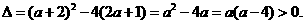
即 <0或
<0或 >4时
>4时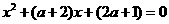 有两个不同的实根
有两个不同的实根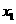 ,
,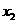 ,不妨设
,不妨设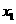 <
<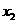
于是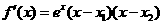 ,从而有下表
,从而有下表
|
x |
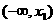 |
x1 |
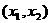 |
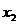 |
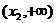 |
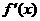 |
+ |
0 |
- |
0 |
+ |
 |
↑ |
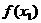 为极大值 为极大值 |
↓ |
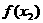 为极小值 为极小值 |
↑ |
即此时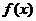 有两个极值点.
有两个极值点.
(2)当△=0即 =0或
=0或 =4时,方程
=4时,方程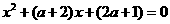 有两个相同的实根
有两个相同的实根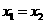
于是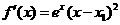
故当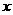 <
<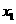 时
时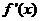 >0,当
>0,当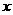 >
>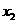 时
时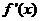 >0,因此
>0,因此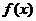 无极值
无极值
(3)当△<0即0< <4时
<4时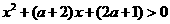
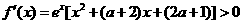 ,故
,故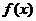 为增函数,此时
为增函数,此时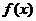 无极值. 因此当
无极值. 因此当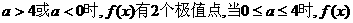 无极值点.
无极值点.
23. (重庆卷)已知aÎR,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com