
题目列表(包括答案和解析)
(17)(本小题满分8分)
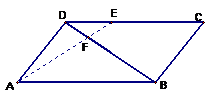
平行四边形ABCD中,已知: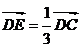 ,
,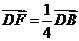 , 求证:A、E、F三点共线。
, 求证:A、E、F三点共线。
(18)(本小题满分10分)
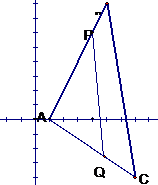
已知△ABC的顶点坐标为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在边AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
(19)(本小题满分10分)在正方体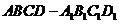 中,E、F、G、H为
中,E、F、G、H为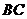 、
、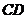 、
、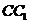 、
、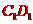 中点.
中点.
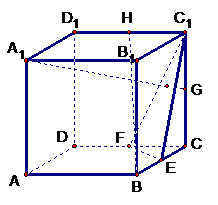 (Ⅰ)求证:
(Ⅰ)求证: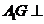 平面
平面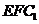 ;
;
(Ⅱ)求证: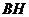 //平面
//平面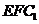 。
。
(20)(本小题满分12分)
已知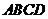 为直角梯形,
为直角梯形,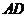 //
//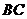 ,
,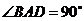 ,
, 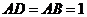 ,
, 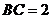 ,
, 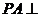 平面
平面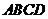 ,
,
(Ⅰ)若异面直线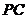 与
与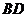 所成的角为
所成的角为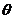 ,且
,且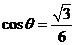 ,求
,求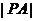 ;
;
(Ⅱ)在(Ⅰ)的条件下,设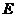 为
为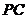 的中点,能否在
的中点,能否在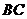 上找到一点
上找到一点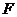 ,使
,使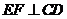 ?
?
(Ⅲ)在(Ⅱ)的条件下,求二面角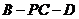 的大小.
的大小.
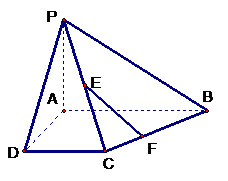
(13)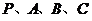 是球
是球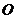 面上的四个点,
面上的四个点,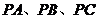 两两垂直,且
两两垂直,且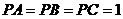 ,则球的体积为__________.
,则球的体积为__________.
(14)设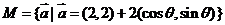 ,
,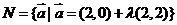 ,则
,则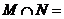
(15)已知: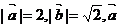 与
与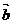 的夹角为45°,要使
的夹角为45°,要使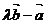 与
与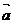 垂直,则
垂直,则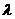 =
.
=
.
(16)向量的命题:①若非零向量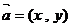 ,向量
,向量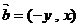 ,则
,则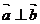 ;②四边形ABCD是菱形的充要条件是
;②四边形ABCD是菱形的充要条件是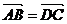 且
且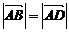 ;③若点G是
;③若点G是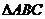 的重心,则
的重心,则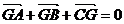 ④
④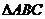 中,
中,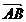 和
和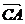 的夹角为
的夹角为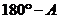 ,其中正确的命题序号是 __________.
,其中正确的命题序号是 __________.
(1)已知向量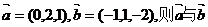 的夹角为
的夹角为
(A)0° (B)45°
(C)90° (D)180°
(2)在空间四边形ABCD中,AB=BC,AD=DC,则对角线AC与BD所成角的大小是
(A)90° (B)60° (C)45° (D)30°
(3)将函数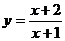 的图象按向量
的图象按向量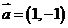 平移后所得图象的函数解析式为
平移后所得图象的函数解析式为
(A)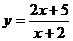 (B)
(B)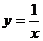 (C)
(C)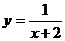 (D)
(D)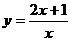
(4)已知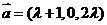 ,
,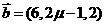 ,若
,若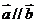 ,则
,则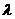 与
与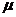 的值分别为
的值分别为
(A)-5,-2 (B)5,2
(C)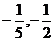 (D)
(D)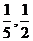
(5)若向量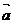 、
、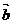 的坐标满足
的坐标满足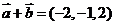 ,
,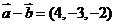 ,则
,则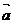 ·
·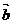 等于
等于
(A)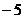 (B)
(B)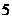 (C)
(C)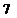 (D)
(D)
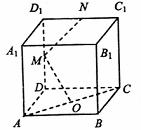 (6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
(6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
是棱DD1、D1C1的中点,则直线OM
(A)是AC和MN的公垂线
(B)垂直于AC,但不垂直于MN
(C)垂直于MN,但不垂直于AC
(D)与AC、MN都不垂直
(7)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的球面距离为(地球半径为R)
(A)R (B)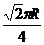 (C)
(C)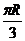 (D)
(D)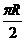
(8)如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为
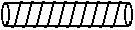 (A)61cm
(B)
(A)61cm
(B)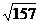 cm
cm
(C)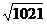 cm (D)
cm (D)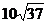 cm
cm
(9)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
(A)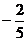 (B)
(B)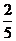 (C)
(C)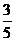 (D)
(D)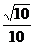
(10)平面内有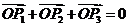 且
且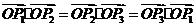 ,则
,则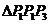 一定是
一定是
(A)钝角三角形 (B)直角三角形
(C)等腰三角形 (D)等边三角形
(11)在棱长为2的正方体AC1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离是
(A)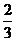 (B)
(B)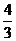 (C)
(C)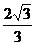 (D)
(D)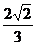
(12)设PA,PB,PC是从点P引出的三条射线,每两条的夹角都等于60°,则直线PC与平面APB所成角的余弦值是
(A)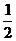 (B)
(B)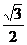 (C)
(C)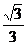 (D)
(D)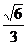
(17)(本小题满分8分)设数列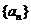 是等比数列,
是等比数列,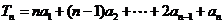 ,已知
,已知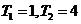 , (1)求数列
, (1)求数列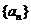 的首项和公比;(2)求数列
的首项和公比;(2)求数列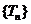 的通项公式。
的通项公式。
(18)(本小题满分10分)已知数列 {an} 的各项均为正数,且满足a2=5,
an+1 = an2-2n an+2,(n Î N*). 推测并证明an的通项公式.
(19)(本小题满分10分)已知数列{an}中,a1 =1,前 n 项和为Sn,且点(an,an+1)在直线
x-y+1=0上. 计算+++…+.
(20)(本小题满分12分)某县与沙漠化进行长期的斗争. 全县面积为 p, 2002 年底绿化率达 ,从 2003 年开始,每年绿化原有沙漠面积的 ,但与此同时,原有绿化面积的 被沙化. 设2002 年底的绿化面积为 a1,经过 n 年后的绿化面积为 an+1 .
(I) 求2003年底的绿化面积
(II ) 经过多少年后,绿化率达?
(13) 已知{an}为等差数列,a1 =2, S10=110. 设an =log0.5 bn ( n Î N*),则{bn}的各项和为 .
(14) 微处理器在诞生后的25年之内,非常准确地遵循“摩尔定律”:半导体芯片每18个月集成度翻番,价格减半. 半导体芯片价格降低,必然导致电脑价格降低. 若每4年电脑的价格降低三分之一,则现价为8100元的电脑12年后价格可能降为 .
(15) 在等比数列中,a9 + a10 = a (a ≠ 0), a19 + a20 = b,则a99 + a100等于 .
(16) 对于n Î N*,若{an}是等差数列,则数列{}也是等差数列.类比上述性质,相应地,若{bn}是正项等比数列,则数列 也是等比数列.
(1) 等差数列 -3,1,5,…的第15 项的值是 (A) 40 (B) 53 (C) 63 (D) 76
(2) 等差数列{an} 中,a3 =2,则该数列的前5项的和为 (A)10 (B) 16 (C) 20 (D)32
(3) 数列 1, , , … , 的各项和为
(A) (B) (C) (D)
(4) 已知数列{an}满足a1 =0,an+1 = an+2n,那么a2005的值是 (A)2003×2004 (B)2004×2005 (C) 20052 (D) 2005×2006
(5) 已知数列 {an}(n Î N)中,a1 = 1,an+1 = ,则an 为 (A) 2n-1 (B) 2n + 1 (C) (D)
(6) 在等比数列 {an} 中, a7 a11 =6, a4 +a14 =5, 则=
(A) (B) (C) 或 (D) -或-
(7) =
(A)0 (B) (C)1 (D) 不存在
(8) 小丁储备2008年赴京观看奥运会的费用,他从2001年起到2007年,每年元旦到银行存入a元一年定期储蓄,若年利率r保持不变,且每年存款到期自动转存新的一年定期. 到2008年元旦将所有的存款和利息悉数取出,可提取
(A) a(1+r)8元 (B) [(1+r)7-(1+r)]元 (C) [(1+r)8-1]元 (D) [(1+r)8-(1+r)]元
(9) 已知{an}是等差数列,{bn}是正项等比数列,其公比q≠1,若a1 = b1,a11 = b11,则 (A) a6<b6 (B) a6 >b6 (C) a6≤ b6 (D) a6≥b6
(10) 等差数列{an}的前n项和为Sn,若a1 >0,S4 =S8,则当Sn取得最大值时,n的值为
(A) 5 (B)6 (C) 7 (D) 8
(11) 数列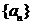 的前n项和为
的前n项和为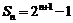 ,那么该数列前2n项中所有奇数位置的项的和为
,那么该数列前2n项中所有奇数位置的项的和为
(A)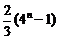 (B)
(B)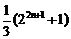 (C)
(C)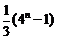 (D)
(D)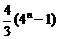
(12) 等差数列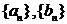 的前n项的和分别为
的前n项的和分别为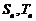 ,若
,若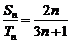 ,则
,则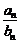 =
=
(A)1
(B)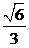 (C)
(C)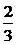 (D)
(D)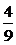
(17)(8分)已知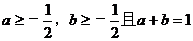 ,求证
,求证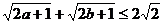
(18)(10分)解关于x的不等式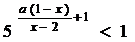
(19)(12分)某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修保养、费用12万元,从第二年开始,每年的维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理方案有两种:(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;(2)当盈利额达到最大值时,以12万元价格处理该机床,问用哪种方案处理较合算?请说明理由.
(20)(12分)已知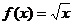 ,g(x)=x+a (a>0)
,g(x)=x+a (a>0)
(1)当a=4时,求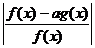 的最小值
的最小值
(2)当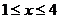 时,不等式
时,不等式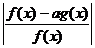 >1恒成立,求a的取值范围.
>1恒成立,求a的取值范围.
(13)已知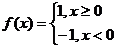 ,则不等式xf(x)+x
,则不等式xf(x)+x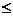 2的解集为
2的解集为
(14)使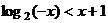 成立的x的范围是
成立的x的范围是
(15)若正数a,b满足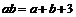 ,则a+b的取值范围是
,则a+b的取值范围是
(16)y=f(x)是R上的减函数,其图象经过点A(0,1)和B(3,-1),则不等式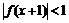 的解集是
.
的解集是
.
(1)不等式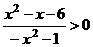 的解集是
的解集是


(2)与不等式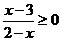 同解的是
同解的是
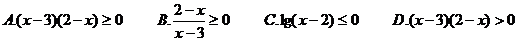
(3)当x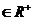 时,下列各函数中,最小值为2的是
时,下列各函数中,最小值为2的是
A. y=x2-2x+4 B. y=x+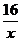 C. y=
C. y=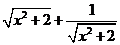 D .y=x+
D .y=x+
(4)已知a<0,a+b>0,则下列不等式中成立的是
A.ab+a2>0 B.ab-a2>0 C.ab+b2<0 D.ab-b2<0
(5)设f(x)=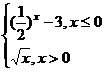 ,已知f(a)>1,则实数a的范围是
,已知f(a)>1,则实数a的范围是
A.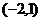 B.
B.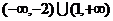 C.
C.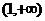 D.
D.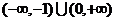
(6)若p,q,m是三个正数,且q<100,现把m增加p%,再把所得的结果减少q%,这样所得的数仍大于m,那么必须且只需
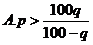 B.
B.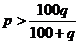 C.
C.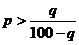 D.p>q
D.p>q
(7)设a1,b1,c1,a2,b2,c2均为非零实数,不等式a1x2+b1x+c1>0,a2x2+b2x+c2>0的解集分别为集合M和N,那么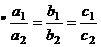 ”是
”是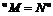 的
的
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
(8)对一切不等式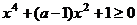 恒成立,则a的取值范围是
恒成立,则a的取值范围是
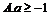 B.
B.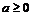 C.
C.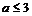 D.
D.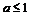
(9)若不等式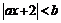 的解集为(-1,2),则实数a等于
的解集为(-1,2),则实数a等于
A.8 B.2 C.-4 D.-8
(10)若关于x的不等式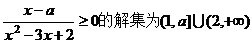 ,则实数a的取值范围是
,则实数a的取值范围是
A.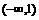 B.
B.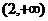 C.(1,2)
D.[1,2]
C.(1,2)
D.[1,2]
(11)已知α、β是关于x的方程x2+mx+m+3=0的两个实根,则α2+β2的最小值是
A.-7 B.2 C.18 D.20
(12)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形式一定是
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
(17)(本题满分8分)
已知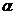 是第二象限角,且
是第二象限角,且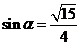 ,求
,求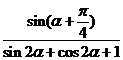 的值.
的值.
(18)(本题满分10分)
已知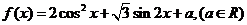
(I)若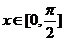 时,
时,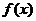 最大值为4,求
最大值为4,求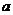 的值
的值
(II)在(I)的条件下,求满足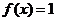 且
且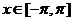 的
的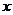 的集合
的集合
(19)(本题满分10分)
在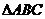 中,
中,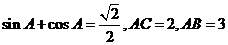 ,求
,求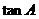 的值和
的值和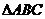 的面积
的面积
(20)(本题满分12分)已知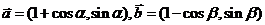 ,
,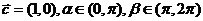 ,
,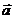 与
与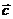 的夹角为
的夹角为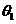 ,
,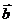 与
与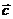 的夹角为
的夹角为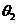 ,且
,且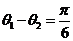 ,求
,求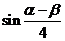 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com