
题目列表(包括答案和解析)
(13) 与直线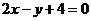 平行的抛物线
平行的抛物线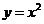 的切线方程是
。
的切线方程是
。
(14)
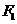 、
、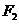 是椭圆C:
是椭圆C: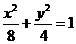 的焦点,在C上满足
的焦点,在C上满足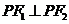 的点
的点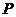 的个数为 。
的个数为 。
(15) 函数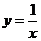 的图象是平面上到两定点的距离之差的绝对值等于定长的点的轨迹,则这个定长为
。
的图象是平面上到两定点的距离之差的绝对值等于定长的点的轨迹,则这个定长为
。
(16) 过点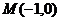 的直线
的直线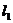 与抛物线
与抛物线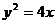 交于
交于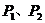 两点,记线段
两点,记线段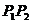 的中点为
的中点为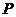 ,过点
,过点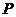 和这个抛物线的焦点
和这个抛物线的焦点 的直线为
的直线为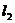 ,
,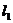 的斜率为
的斜率为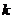 ,则直线
,则直线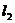 的斜率与直线
的斜率与直线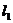 的斜率之比可表示为
的斜率之比可表示为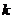 的函数
的函数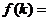 __ .
__ .
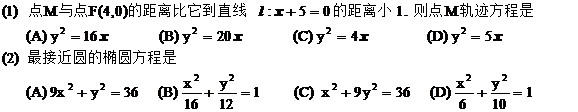
(3) 若椭圆的离心率为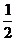 ,左焦点到相应的左顶点的距离为1,则椭圆的长轴长是
,左焦点到相应的左顶点的距离为1,则椭圆的长轴长是
(A)4
(B)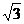 (C) 2 (D)
(C) 2 (D) 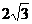
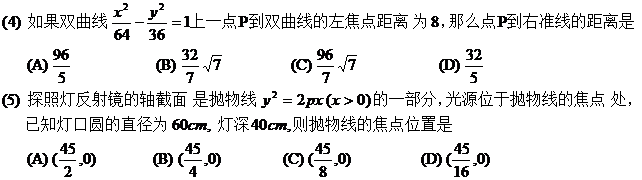 (6) 若抛物线
(6) 若抛物线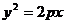 与
与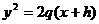 有共同焦点,则
有共同焦点,则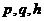 的关系是
的关系是
(A)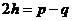 (B)
(B)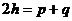 (C)
(C)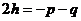 (D)
(D)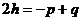
(7) 过双曲线的一个焦点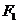 作垂直于实轴的弦
作垂直于实轴的弦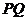 ,
, 是另一个焦点,若
是另一个焦点,若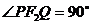 。则此双曲线的离心率为
。则此双曲线的离心率为
(A)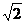 (B)
(B)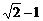 (C)
(C)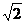 +1 (D)
+1 (D)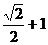
(8) 若椭圆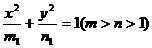 和双曲线
和双曲线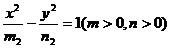 有公共的焦点
有公共的焦点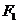 ,
, ,
,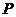 是它们的一个公共点,则
是它们的一个公共点,则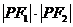 的值是
的值是
(A)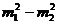 (B)
(B) 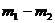 (C)
(C)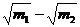 (D)
(D)
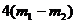
(9) 若焦点坐标为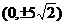 的椭圆与直线
的椭圆与直线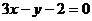 相交所得的弦中点的横坐标是
相交所得的弦中点的横坐标是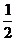 ,则此椭圆的标准方程是
,则此椭圆的标准方程是
(A)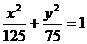 (B)
(B) 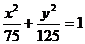 (C)
(C)  (D)
(D) 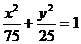
(10) 我国某颗人造地球卫星的运行轨迹是以地心F为一个焦点的椭圆,若它的近地点A距离地面m公里,远地点B距离地面M公里,地球半径为R公里,则该卫星轨迹的离心率e是
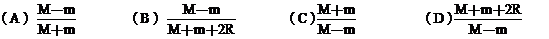
(11) 与双曲线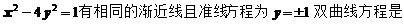

(12) 已知抛物线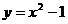 上一定点B(-1,0)和两个动点
上一定点B(-1,0)和两个动点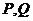 ,当
,当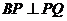 时,点
时,点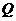 的横坐标的取值范围是
的横坐标的取值范围是
(A)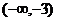 (B)
(B) 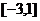
 (C)
(C) 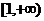 (D)
(D) 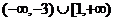
(17) (满分8分)已知随机变量 x 的分布列如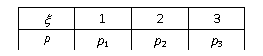 下,且已知 Ex = 2,Dx = 0.5,
下,且已知 Ex = 2,Dx = 0.5,
求:
(I) p1、p2、p3
(II) P(-1 < x < 2)、P(1 < x < 2)
(18) (满分10分)设数列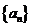 是等比数列,
是等比数列,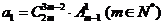 ,公比
,公比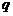 是
是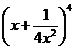 的展开式中的第二项(按
的展开式中的第二项(按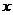 的降幂排列).
的降幂排列).
(1)求常数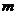 与
与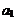 的值;
的值;
(2)用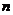 ,
,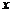 表示数列{
表示数列{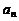 }的前项和
}的前项和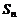 ;
;
(3)若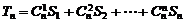 ,用
,用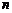 ,
,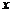 表示
表示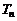 .
.
(19) (满分10分)某保险公司开设了一项保险业务,若在一年内事件 E 发生,该公司要赔偿10000 元,设一年内 E 发生的概率为 0.001,要使公司收益的期望值为 500 元,公司应要求顾客交多少保险金?
(20)(满分12分)将15名转学生(12位男生3位女生)平均分到高三级甲、乙、丙三个班.
(I) 每班各分配到一名女生的概率是多少?
(II) 3名女生同去一个班的概率是多少?
 (13) 为获知野生动物保护区内某种野生动物的数量,工作人员逮到该种动物1200只,作标记后放回. 若干天后,再逮到该种动物1000只,数得当中有100只作过标记. 按概率方法估算,保护区内这种动物有 只.
(13) 为获知野生动物保护区内某种野生动物的数量,工作人员逮到该种动物1200只,作标记后放回. 若干天后,再逮到该种动物1000只,数得当中有100只作过标记. 按概率方法估算,保护区内这种动物有 只.
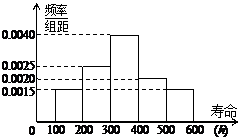
(14) 某电子元件厂对一批新产品的使用寿命进行检
验,质检科抽取了一个容量为100的样本,经
检测统计后,绘制出了该产品使用寿命的频率
分布直方图(如图),估计这批新产品的使用
寿命在400h以上的概率是 .
(15) 设 (+x) 10 = a0 + a1 x + a2 x 2 + … + a10 x 10,则 (a0 + a2 + a4 + … + a10) 2-(a1 + a3 + a5 + … + a9) 2 的值为 .
(16) 三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为凹数,如524,746等,那么各位上无重复数字的三位凹数共有 个.
(1)已知随机变量 x 服从二项分布,且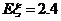 ,
,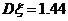 ,则二项分布的参数
,则二项分布的参数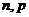 的值为
的值为
(A)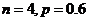 (B)
(B) 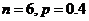 (C)
(C) 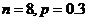 (D)
(D)
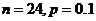
(2)对总数为N的一批零件抽取一个容量为30的样本,若每个零件被抽到的概率为0.25,则N的值为
(A) 100 (B) 120 (C) 150 (D) 200
(3)10张奖券中有2张是有奖的,甲、乙两人中各抽1张,甲先抽,然后乙抽,设甲中奖的概率为p1,乙中奖的概率为p2,那么
(A) p1 > p2 (B) p1 < p2 (C) p1 = p2 (D) p1, p2大小不确定
(4)若x Î N,且x<55,则(55-x)(56-x)…(68-x)(69-x)=
(A) A (B) A (C) A (D) A
(5)学校黑板报设有9个学科专栏,由高中三个年级各负责3个专栏,其中数学由高三级负责. 则不同的分工方法种数为
(A) 1680 (B) 560 (C) 280 (D) 140
(6)某年级8个班协商组建年级篮球队,共需10名队员,每个班至少有1个名额,不同的名额分配方案种数为
(A) 16 (B) 24 (C) 28 (D) 36
(7)把红、黄、绿、蓝四张纸牌随机分发给甲、乙、丙、丁四个人,每人分得一个. 事件“甲分得红牌”与事件“乙分得红牌”是 (A) 对立事件 (B) 不可能事件
(C) 互斥但非对立事件 (D) 以上答案均不对
(8)氨基酸的排列顺序是决定蛋白质多样性的原因之一,某肽链由7种不同的氨基酸构成,研究人员试验每次改变其中三种氨基酸的位置,其他四种位置不变,则试验的总次数为
(A) 126 (B) 70 (C) 35 (D)210
(9)将两名男生、五名女生的照片排成一排贴在光荣榜上,恰有三名女生的照片贴在两名男生的照片之间的概率为
(A) (B) (C) (D)
(10)3位好友不约而同乘一列火车. 该列火车有10节车厢,那么至少有2人在同一节车厢相遇的概率为
(A) (B) (C) (D)
(11)设随机变量ξ的概率分布列为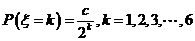 ,其中c为常数,则
,其中c为常数,则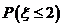 的值为
的值为
(A)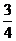 (B)
(B)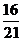 (C)
(C)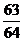 (D)
(D)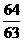
(12)某仪表显示屏上有一排7个小孔,每个小孔可显示出0或1,若每次显示其中三个小孔,且相邻的两个小孔不能同时显示,则这个显示屏可以显示不同信号的种数为
(A) 10 (B) 48 (C) 60 (D) 80
22.设函数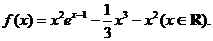
(1)求函数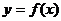 的单调区间;
的单调区间;
(2)求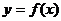 在[-1,2]上的最小值;
在[-1,2]上的最小值;
21.已知定点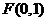 和直线
和直线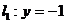 ,过定点F与直线
,过定点F与直线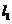 相切的动圆圆心为点C。
相切的动圆圆心为点C。
(1)求动点C的轨迹方程;
(2)过点F在直线l2交轨迹于两点P、Q,交直线l1于点R,求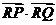 的最小值。
的最小值。
20. 济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点,一位客人浏览这四个景点的概率分别是0.3,0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设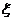 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求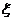 =0对应的事件的概率;
=0对应的事件的概率;
(2)求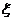 的分布列及数学期望。
的分布列及数学期望。
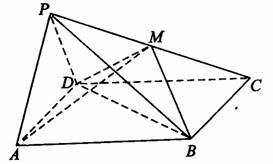
19.如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA//平面BDM,
(1)求证:M为PC的中点;
(2)求证:面ADM⊥面PBC。
18.已知数列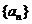 的各项为正数,前
的各项为正数,前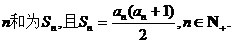
(1)求证:数列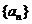 是等差数列;
是等差数列;
(2)设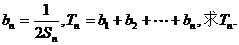
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com