
题目列表(包括答案和解析)
(1)若集合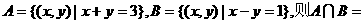

(2)条件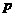 :|x|>1,条件q:x<-2,则p是q的
:|x|>1,条件q:x<-2,则p是q的
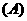 必要不充分条件
必要不充分条件 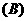 充分不必要条件
充分不必要条件  充要条件
充要条件 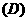 非充分非必要条件
非充分非必要条件
(3)已知f(x)=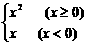 ,
,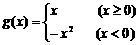 ,则
,则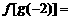
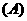 -4
-4
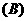 4
4
 -2
-2
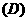 2
2
(4)定义集合A、B的一种运算:A*B={x|x=x1+x2,x1∈A,x2∈B},若A={1,2,3}, B={1,2},则A*B中的所有元素之和为
(A)21 (B)18 (C)14 (D)9
(5)已知函数y=tan(2x+φ)的图象过点(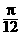 ,0),则φ可以是 ( )
,0),则φ可以是 ( )
(A)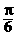 (B)-
(B)-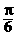 (C)-
(C)-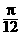 (D)
(D)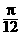
(6)函数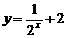 的反函数是
的反函数是


(7)设全集为R,A=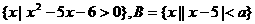 (a为常数),且11∈B,则
(a为常数),且11∈B,则
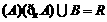
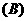
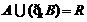

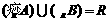
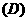
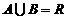
(8)函数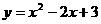 在区间
在区间 上有最大值3,最小值2,则
上有最大值3,最小值2,则 的取值范围是
的取值范围是

(9)函数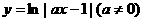 图象的对称轴方程是
图象的对称轴方程是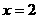 ,那么a等于
,那么a等于

(10)下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间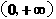 上是减函数;
上是减函数;
(3)是偶函数.这样的函数是
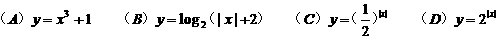
(11)设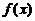 是定义在
是定义在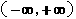 上的函数,对于任意
上的函数,对于任意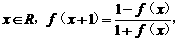 且当
且当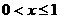 时,
时,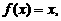 则
则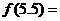


(12)右图所示的某池塘中的浮萍蔓延的面积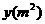 与时间
与时间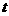 (月)的关系为:
(月)的关系为: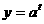 .有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30
.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30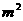 ;③浮萍每月增加的面积都相等;④若浮萍蔓延到
;③浮萍每月增加的面积都相等;④若浮萍蔓延到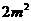 ,
,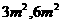 所经过的时间分别为
所经过的时间分别为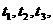 则
则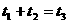 .其中判断正确的个数是
.其中判断正确的个数是

求函数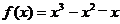 的极值和单调区间.
的极值和单调区间.
(18)(本小题满分10分)
设函数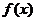 是定义在
是定义在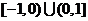 上的奇函数,当
上的奇函数,当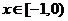 时,
时,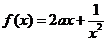
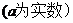
(Ⅰ)当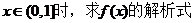 ;
;
(Ⅱ)若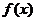 在
在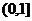 上为增函数,求
上为增函数,求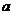 的取值范围.
的取值范围.
(19)(本小题满分10分)
设函数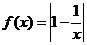 ,点P(x0,y0)
,点P(x0,y0)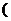 0<x0<1
0<x0<1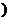 在曲线
在曲线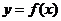 上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
(20)(本小题满分12分)
某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品则损失100元.已知该厂制造电子元件过程中,次品率p与日产量x的函数关系是: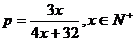 .
.
(I)将该厂的日盈利额T(元)表示为日产量x(件)的函数;
(II)为获得最大盈利,该厂的日产量应为多少件?
(14)函数y=x-2sinx在(0, 2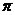 )内的单调增区间为
.
)内的单调增区间为
.
(15)曲线y=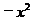 上的点到直线2x-y+3=0的最短距离为
.
上的点到直线2x-y+3=0的最短距离为
.
(16)向高为8m,底面边长为8m的倒置正四棱锥形的容器内注水,其速度为每分钟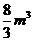 ,则
当水深为5m时,水面上升的速度为
.
,则
当水深为5m时,水面上升的速度为
.
(1)已知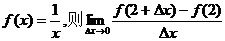 的值是
的值是
(A)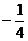 (B)2
(C)
(B)2
(C)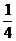 (D)-2
(D)-2
(2)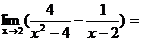
(A)0
(B)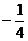 (C)
(C)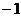 (D)
(D)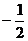
(3)已知曲线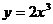 ,则过点(1,2)的切线的斜率是
,则过点(1,2)的切线的斜率是
(A)2 (B)4 (C)6 (D)8
(4)函数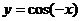 的导数是
的导数是
(A)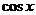 (B)
(B)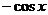 (C)
(C)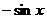 (D)
(D)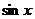
(5)若函数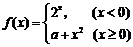 为R上的连续函数,则a 的值为
为R上的连续函数,则a 的值为
(A)2 (B)1 (C)0 (D)-1
(6)下列给出的四个命题中,正确的命题是
①若函数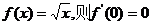
②若函数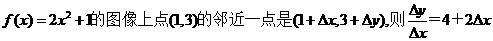
③瞬时速度是动点位移函数S(t)对时间t的导数
④曲线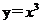 在点(0,0)处没有切线
在点(0,0)处没有切线
(A)①② (B)②③ (C)①②③ (D)②③④
(7)函数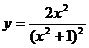 的导数是
的导数是
(A)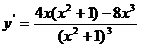 (B)
(B)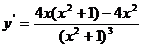
(C)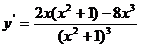 (D)
(D)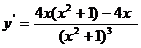
(8)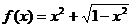 为增函数的区间是
为增函数的区间是
(A)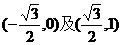 (B)
(B)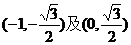
(C)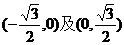 (D)
(D)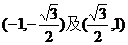
(9)函数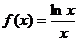 的最大值为
的最大值为
(A)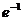 (B)e
(C)
(B)e
(C)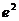 (D)10
(D)10
(10)半径为r的圆形铁板,受热膨胀,半径r为时间t的函数,其导数(半径膨胀率)为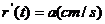 那么其面积的膨胀率
那么其面积的膨胀率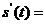
(A)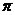 (B)
(B)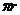 (C)
(C)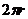 (D)
(D)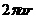
(11)若f(x)是在(-L,L)内的可导的偶函数,且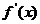 不恒为0,则
不恒为0,则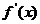
(A)必定是(-L,L)内的偶函数
(B)必定是(-L,L)内的奇函数
(C)必定是(-L,L)内的非奇非偶函数
(D)可能是(-L,L)内的奇函数,可能是偶函
(12)已知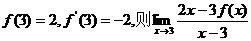 的值是
的值是
(A)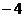 (B)0
(C)8
(D)不存在
(B)0
(C)8
(D)不存在
(17) ( 本题满分12分 )
已知函数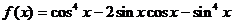
(I)求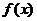 的最小正周期;
的最小正周期;
(II)若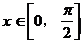 ,求
,求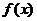 的最大值,最小值.
的最大值,最小值.
(18) ( 本题满分12分 )
已知一台机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作.一周五天工作日里无故障可获利10万元,发生一次故障可获利5万元,发生两次故障没有利润,发生三次或三次以上故障就要亏损2万元.这台机器在一周内平均获利多少?
(19) ( 本题满分12分 )
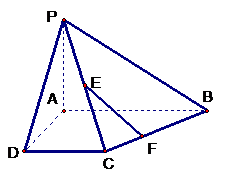
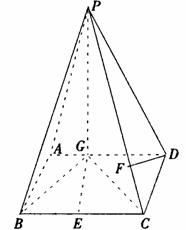 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=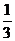 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为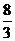 .
.
(Ⅰ)求异面直线GE与PC所成的角;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求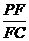 的值.
的值.
(20) ( 本题满分12分 )
已知等差数列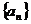 的前n 项之和为Sn,令
的前n 项之和为Sn,令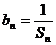 ,且
,且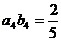 ,S6-S3=15.
,S6-S3=15.
(Ⅰ)求数列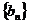 的通项公式与它的前10项之和;
的通项公式与它的前10项之和;
(Ⅱ)若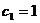 ,
,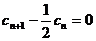 ,
,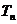 =
=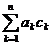 ,求
,求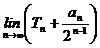 的值.
的值.
(21) ( 本题满分12分 )
已知点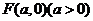 ,动点
,动点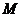 、
、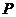 分别在
分别在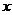 、
、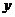 轴上运动,满足
轴上运动,满足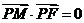 ,
,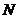 为动点,并且满足
为动点,并且满足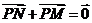 .
.
(Ⅰ)求点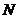 的轨迹
的轨迹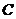 的方程;
的方程;
(Ⅱ)过点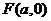 的直线
的直线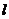 (不与
(不与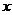 轴垂直)与曲线
轴垂直)与曲线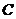 交于
交于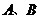 两点,设点
两点,设点 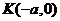 ,
,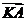 与
与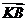 的夹角为
的夹角为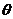 ,求证:
,求证: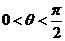 .
.
(22) ( 本题满分14分 )
函数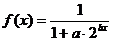 的定义域为R,且
的定义域为R,且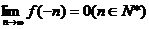
(Ⅰ)求证: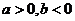 ;
;
(Ⅱ)若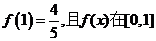 上的最小值为
上的最小值为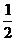 ,试求f(x)的解析式;
,试求f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下记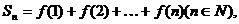 试比较
试比较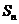 与
与
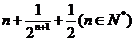 的大小并证明你的结论.
的大小并证明你的结论.
(13)已知点P在抛物线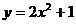 上运动,定点A(0,-1),若点M分
上运动,定点A(0,-1),若点M分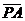 所成的比为2,则动点M的轨迹方程是
.
所成的比为2,则动点M的轨迹方程是
.
(14) 一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,测的刹车后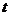 秒内列车前进的距离为
秒内列车前进的距离为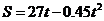 米,则列车刹车后 秒车停下来,期间列车前进了
米.
米,则列车刹车后 秒车停下来,期间列车前进了
米.
 (15)在测量学中,把斜坡的坡面与水平面所成二
(15)在测量学中,把斜坡的坡面与水平面所成二
面角的大小叫做坡角.若要将坡长为100 m 、 100 m
坡角为450的坡面,改造成坡角为300的坡面, 450 300
则坡底要伸长 m.
(16) 设有两个命题: ① 不等式 + 4 >m> 2x-x2对一切实数x恒成立;
+ 4 >m> 2x-x2对一切实数x恒成立;
② 函数f(x)=-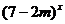 是R上的减函数.
是R上的减函数.
使这两个命题都是真命题的充要条件,用m可表示为 .
(1)计算: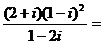 ( )
( )
(A)2 (B)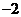 (C)
(C)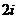 (D)
(D)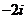
(2)已知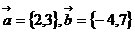 ,则
,则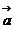 在
在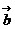 上的射影为
上的射影为
(A) 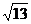 ; (B)
; (B) 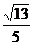 ; (C)
; (C) 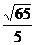 ; (D)
; (D) 
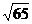
(3)已知a、b为直线,α、β为平面.在下列四个命题中,
① 若a⊥α,b⊥α,则a∥b ; ② 若 a∥α,b ∥α,则a∥b;
③ 若a⊥α,a⊥β,则α∥β; ④ 若α∥b,β∥b ,则α∥β.
正确命题的个数是
(A) 1 (B) 3 (C) 2 (D) 0
(4)函数f(x)=A·tan(ωx+φ)(φ>0)在区间[m,n]上的函数值都小于0,则函数g(x)=A·cot(ωx+φ)在[m,n]上的函数值
(A) 都大于0,且有最大值为g(m) (B) 都小于0,且有最大值为g(m)
(C) 都大于0,且有最小值为g(m) (D) 都小于0,且有最小值为g(m)
 (5)已知函数
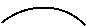
(5)已知函数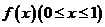 的图象的一段圆弧(如图所示)
的图象的一段圆弧(如图所示)
若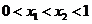 ,则
,则
 (A)
(A)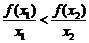 (B)
(B)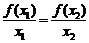
(C)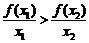 (D)前三个判断都不正确
(D)前三个判断都不正确
(6)对于四条曲线:① 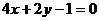 ;②
;② 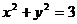 ;③
;③ 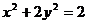 ;
;
④ 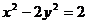 . 其中与直线2 x + y +3=0有交点的所有曲线是
. 其中与直线2 x + y +3=0有交点的所有曲线是
(A) ②,③,④ (B) ①,② (C) ②,④ (D) ①,②,③
(7)将4名司机和8名售票员分配到四辆公共汽车上,每辆车上分别有1名司机和2名售票员,则可能的分配方案种数是
(A)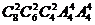 (B)
(B)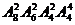 (C)
(C)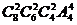 (D)
(D)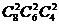
(8)定义在R上的偶函数f(x)在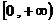 上递增,
上递增,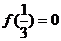 ,则满足
,则满足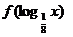 >0的x的取值范围是
>0的x的取值范围是
(A)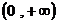 (B)
(B)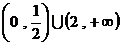 (C)
(C) 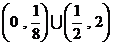 (D)
(D) 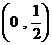
(9)现有一个长方体水箱,从水箱里面量得它的深是30cm,底面的长是25cm,宽是20cm.设0< a ≤8,水箱里盛有深为a cm的水,若往水箱里放入棱长为10cm的立方体铁块,则水深为
(A) 2 cm
(B) 10 cm
(C) (a+2) cm
(D) 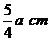
(10)我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F为一个焦点的椭圆,近地点A距地面为m公里,远地点B距地面为n公里.若地球的半径为R公里,则飞船运行轨道的短轴长为
(A) mn (B) 2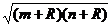 (C) 2nm (D)
(C) 2nm (D) 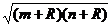
(11)已知函数f(x)的图象过点(0,-5),它的导数f /(x)=4x3-4x,则当f(x)取得最大值-5时,x的值应为
(A) -1 (B) 0 (C) 1 (D) ±1
(12)在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
(A)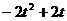 (B)
(B)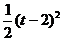 (C)
(C)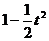 (D)
(D) 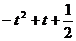
(17)(本小题满分8分)
平行四边形ABCD中,已知: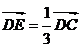 ,
,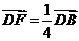 , 求证:A、E、F三点共线。
, 求证:A、E、F三点共线。
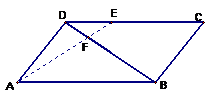
(18)(本小题满分10分)
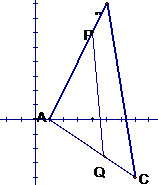
已知△ABC的顶点坐标为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在边AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
(19)(本小题满分10分)在正方体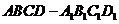 中,E、F、G、H为
中,E、F、G、H为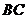 、
、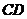 、
、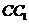 、
、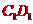 中点.
中点.
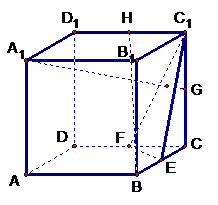 (Ⅰ)求证:
(Ⅰ)求证: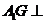 平面
平面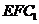 ;
;
(Ⅱ)求证: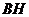 //平面
//平面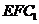 。
。
(20)(本小题满分12分)
已知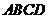 为直角梯形,
为直角梯形,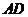 //
//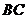 ,
,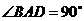 ,
, 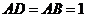 ,
, 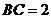 ,
, 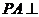 平面
平面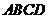 ,
,
(Ⅰ)若异面直线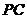 与
与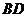 所成的角为
所成的角为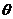 ,且
,且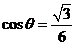 ,求
,求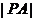 ;
;
(Ⅱ)在(Ⅰ)的条件下,设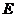 为
为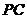 的中点,能否在
的中点,能否在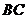 上找到一点
上找到一点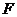 ,使
,使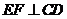 ?
?
(Ⅲ)在(Ⅱ)的条件下,求二面角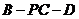 的大小.
的大小.
(13)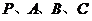 是球
是球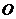 面上的四个点,
面上的四个点,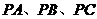 两两垂直,且
两两垂直,且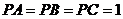 ,则球的体积为__________.
,则球的体积为__________.
(14)设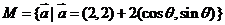 ,
,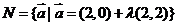 ,则
,则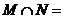
(15)已知: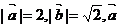 与
与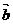 的夹角为45°,要使
的夹角为45°,要使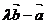 与
与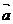 垂直,则
垂直,则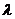 =
.
=
.
(16)向量的命题:①若非零向量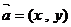 ,向量
,向量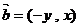 ,则
,则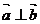 ;②四边形ABCD是菱形的充要条件是
;②四边形ABCD是菱形的充要条件是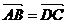 且
且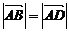 ;③若点G是
;③若点G是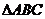 的重心,则
的重心,则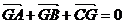 ④
④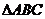 中,
中,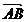 和
和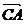 的夹角为
的夹角为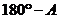 ,其中正确的命题序号是 __________.
,其中正确的命题序号是 __________.
(1)已知向量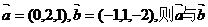 的夹角为
的夹角为
(A)0° (B)45°
(C)90° (D)180°
(2)在空间四边形ABCD中,AB=BC,AD=DC,则对角线AC与BD所成角的大小是
(A)90° (B)60° (C)45° (D)30°
(3)将函数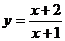 的图象按向量
的图象按向量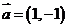 平移后所得图象的函数解析式为
平移后所得图象的函数解析式为
(A)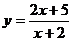 (B)
(B)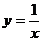 (C)
(C)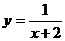 (D)
(D)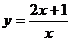
(4)已知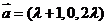 ,
,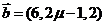 ,若
,若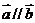 ,则
,则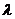 与
与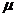 的值分别为
的值分别为
(A)-5,-2 (B)5,2
(C)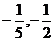 (D)
(D)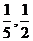
(5)若向量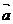 、
、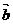 的坐标满足
的坐标满足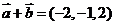 ,
,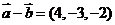 ,则
,则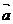 ·
·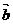 等于
等于
(A)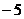 (B)
(B)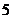 (C)
(C)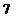 (D)
(D)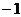
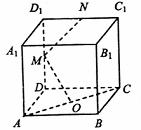 (6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
(6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
是棱DD1、D1C1的中点,则直线OM
(A)是AC和MN的公垂线
(B)垂直于AC,但不垂直于MN
(C)垂直于MN,但不垂直于AC
(D)与AC、MN都不垂直
(7)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的球面距离为(地球半径为R)
(A)R (B)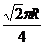 (C)
(C)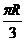 (D)
(D)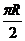
(8)如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为
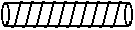 (A)61cm
(B)
(A)61cm
(B)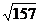 cm
cm
(C)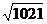 cm (D)
cm (D)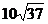 cm
cm
(9)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
(A)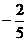 (B)
(B)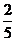 (C)
(C)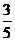 (D)
(D)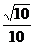
(10)平面内有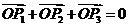 且
且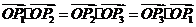 ,则
,则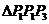 一定是
一定是
(A)钝角三角形 (B)直角三角形
(C)等腰三角形 (D)等边三角形
(11)在棱长为2的正方体AC1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离是
(A)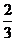 (B)
(B)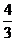 (C)
(C)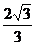 (D)
(D)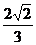
(12)设PA,PB,PC是从点P引出的三条射线,每两条的夹角都等于60°,则直线PC与平面APB所成角的余弦值是
(A)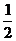 (B)
(B)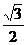 (C)
(C)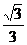 (D)
(D)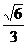
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com