
题目列表(包括答案和解析)
(13)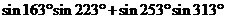 =
.
=
.
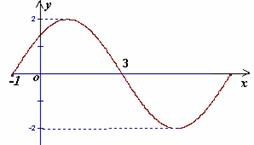 (14)已知
(14)已知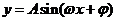 ,
,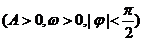 的图象如图所示,则它的解析式为 _____
.
的图象如图所示,则它的解析式为 _____
.
(15)已知函数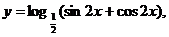 则它的单调递减区间为
.
则它的单调递减区间为
.
(16)函数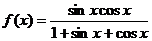 的值域为
.
的值域为
.
(1)如果角2α的终边在x轴上方,那么α的范围是
(A) 第一象限角的集合 (B) 第一或第二象限角的集合
(C) 第一或第三象限角的集合 (D) 第一或第四象限角的集合
(2)若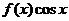 是周期为
是周期为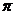 的奇函数,则
的奇函数,则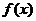 可以是
可以是
(A) 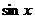 (B)
(B) 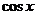 (C)
(C) 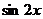 (D)
(D) 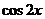
(3))函数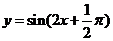 的图像的一条对称轴是
的图像的一条对称轴是
(A)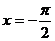 (B)
(B) 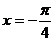 (C)
(C) 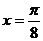 (D)
(D) 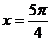
(4)设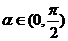 ,若
,若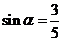 ,则
,则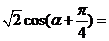
(A)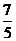 (B)
(B)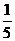 (C)
(C)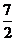 (D)
(D)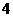
(5)(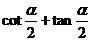 )可化简为
)可化简为
(A) 2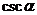 (B)2 (C)
(B)2 (C) 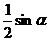 (D)
(D) 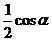
(6)在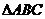 中,“
中,“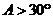 ”是“
”是“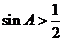 ”的
”的
(A)充分而不必要条件 (B) 必要而不充分条件
(C)充分必要条件 (D) 既不充分也不必要条件
(7)已知点P(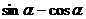 ,
,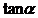 )在第一象限,则在[0,2π)内α的取值范围是
)在第一象限,则在[0,2π)内α的取值范围是
(A)(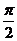 ,
,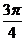 )∪
)∪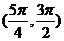 (B)
(B) 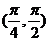 ∪
∪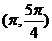
(C) 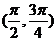 ∪
∪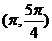 (D)
(D) 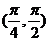 ∪
∪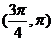
(8) 把函数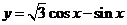 的图像向左平移
的图像向左平移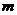 (
(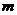
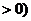 个单位,所得图像关于
个单位,所得图像关于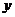 轴对称,则
轴对称,则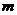 的最小值是
的最小值是
(A)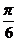 (B)
(B) 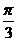 (C)
(C)
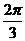 (D)
(D) 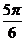
(9)将函数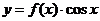 按向量
按向量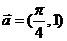 平移,得到函数
平移,得到函数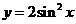 的图象,那么
的图象,那么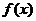 可以是
可以是
(A)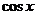 (B)
(B)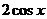 (C)
(C)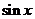 (D)
(D)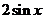
(10)函数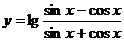 的定义域是
的定义域是
(A)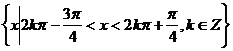 (B)
(B)
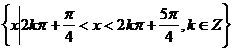
(C) 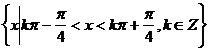 (D)
(D) 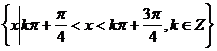
(11)在△ABC中,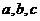 分别为角
分别为角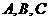 的对边,若
的对边,若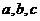 成等差数列,
成等差数列,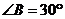 ,
,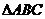 的面积为
的面积为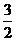 ,则
,则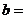
(A)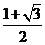 (B)
(B)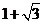 (C)
(C)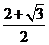 (D)
(D)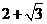
(12)定义在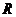 上的函数
上的函数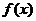 既是偶函数,又是周期函数,若
既是偶函数,又是周期函数,若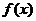 的最小正周期是
的最小正周期是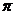 ,且当
,且当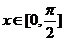 时,
时,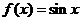 ,则
,则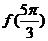 的值为
的值为
(A)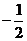 (B)
(B)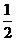 (C)
(C)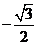 (D)
(D)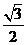
(17)(本小题满分8分)
已知直线l垂直于直线3x + 2y-6 = 0,且在两坐标轴上的截距之和为-2,求直线l的方程。
(18)(本小题满分10分)
直线l过点(1,0),且被两平行直线3x + y-6 = 0和3x + y + 3 = 0所截得的线段长为9,求直线l的方程。
(19)(本小题满分10分)
已知直线l1:5x-2y + 3m(3m + 1) = 0与l2:2x + 6y-3m(9m +20) = 0。当m为何值时,两直线l1,l2的交点到直线4x-3y-12 = 0的距离最小?最小值为多少?
(20) (本小题满分12分)
已知已知过点A(1,1)且斜率为-m(m>0)的直线l与x,y轴分别交于P,Q,过P,Q作直线2x + y = 0的垂线,垂足为R,S.求四边形PRSQ的面积的最小值。
(13)直线l1与l2的斜率是方程6x2 + x-1 = 0的两根,则直线l1和l2的夹角是 .
(14)若直线l1:ax + 2y + 6 = 0与直线l2:x + (a-1)y + a2-1 = 0,则l1∥l2时,a =
l1⊥l2时,a = .
(15) 直线l1:bx-2y + 2 = 0和直线l2:2x + 6y + c = 0相交于点(1,m),且l1到l2的角为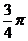 ,则b,c,m的值分别为
.
,则b,c,m的值分别为
.
(16)直线l1过点P1(4,2),直线l2过点P2(-1,3),若l1∥l2,且l1与l2间距离最大,此时l1的方程是 .
(1)下列命题不正确的是
A、若直线l1∥l2,则k1 = k2 B、若直线l1⊥l2,则k1·k2 =-1
C、若k1 = k2,则l1∥l2 D、若k1·k2 =-1,则l1⊥l2
(2)直线l1:2x + (m + 1)y + 4 = 0与直线l2:mx + 3y-2 = 0平行,则m的值为
A、2 B、-3 C、2或-3 D、-2或-3
(3)已知直线3ax-y = 1与直线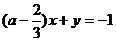 垂直,则a的值为
垂直,则a的值为
A、-1或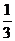 B、1或
B、1或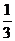 C、-
C、-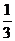 或-1 D、-
或-1 D、-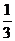 或1
或1
(4)以A(1,-1),B(-2,0)为端点的线段的垂直平分线的方程是
A、3x + y-4 = 0 B、3x + y + 4 = 0
C、3x-y + 1 = 0 D、3x-y -1 = 0
(5)直线x + y-1 = 0到直线x·sin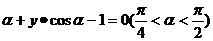 的角是
的角是
A、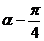 B、
B、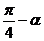 C、
C、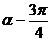 D、
D、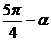
(6)已知直线l1: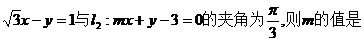
A、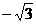 B、
B、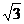 或0 C、
或0 C、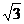 或
或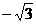 D、
D、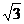 或
或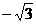 或0
或0
(7)在直线l:3x-4y-27 = 0上到点P(2,1)距离最近的点的坐标是
A、(5,-3) B、(9,0) C、 D、(-5,3)
(8)m,n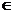 R,直线
R,直线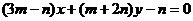 过定点
过定点
A、(-1,3) B、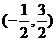 C、
C、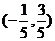 D、
D、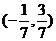
(9已知直线mx + 4y-2 = 0与2x-5y + n = 0垂直,垂足为(1,P),则m-n + p的值为
A、24 B、20 C、0 D、-4
(10)点(0,2)关于直线x + 2y-1 = 0的对称点是
A、(-2,0) B、(,0) C、(0,-1)
D、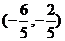
(11)若点(4,a)到直线4x-3y = 1的距离不大于3,则a的取值范围是
A、[0,10] B、(0,10) C、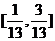 D、
D、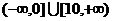
(12)入射光线在直线l1:2x-y-3 = 0上,经过x轴反射,反射光线在直线l2上,再经过y轴反射到直线l3上,则直线l3的方程为
A、x-2y + 3 = 0 B、2x-y + 3 = 0 C、2x + y-3 = 0 D、2x-y + 6 = 0
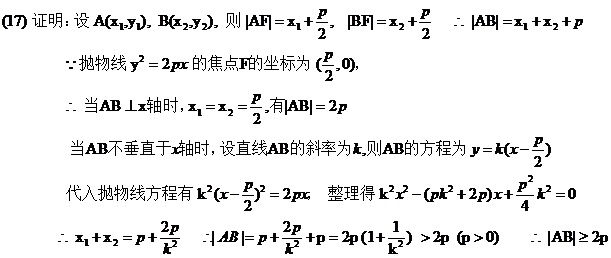 (18).设中心为O,正西的观测点为A,正东的观测点为B,正北的观测点为C,以O为原点建立直角坐标系,由已知巨响的位置M在AC的中垂线上,且在以A、B为焦点,实轴为1360的双曲线左支上,AC的中垂线:
(18).设中心为O,正西的观测点为A,正东的观测点为B,正北的观测点为C,以O为原点建立直角坐标系,由已知巨响的位置M在AC的中垂线上,且在以A、B为焦点,实轴为1360的双曲线左支上,AC的中垂线: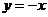 ① 双曲线:
① 双曲线: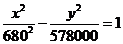 ②
②
解①②得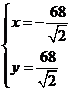 ∴巨响位于西北方向,距中心为68m。
∴巨响位于西北方向,距中心为68m。
(19) 解(I)设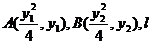 过顶点E(-1,0),则
过顶点E(-1,0),则
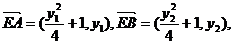 由E、A、B三点共线,知
由E、A、B三点共线,知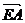 //
//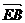 , 所以,
, 所以,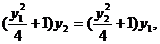 即
即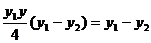 ,因为
,因为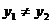 ,所以
,所以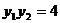
所以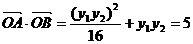 (与
(与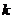 无关).
无关).
(II)设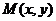 ,则由
,则由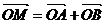 ,
,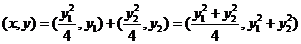
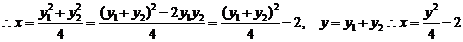 即
即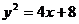 又
又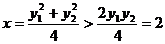 所以点
所以点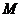 的轨迹方程为
的轨迹方程为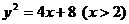 .
.
解法二提示:设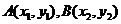 ,则
,则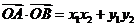 联立方程组
联立方程组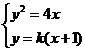
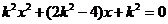 由韦达定理得
由韦达定理得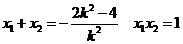
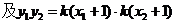 可解得
可解得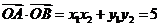
(20) (I)由题意得:
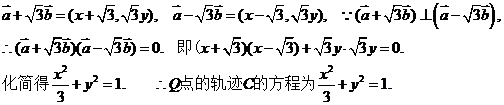
(II)由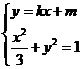 得
得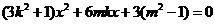 ,
,
由于直线与椭圆有两个不同的交点,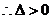 ,即
,即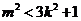 ①
①
(1)当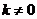 时,设弦MN的中点为
时,设弦MN的中点为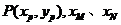 分别为点M、N的横坐标,则
分别为点M、N的横坐标,则
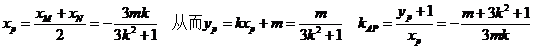
又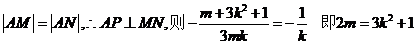 ②,将②代入①得
②,将②代入①得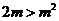 ,解得
,解得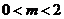 , 由②得
, 由②得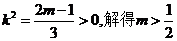 , 故所求的
, 故所求的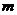 取值范围是
取值范围是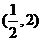 .
.
(2)当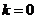 时,
时,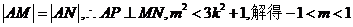 .
.
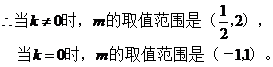
(13) 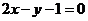 (14) 2
(15)
(14) 2
(15) 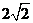 (16)
(16) 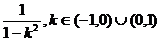
(1)A (2)B (3)A (4)A (5)C (6)D (7)C (8)B (9)C (10)B (11)D (12)D
(八)圆锥曲线 答案

(18) (本小题满分10分)
某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到该巨响的时间比其他两观测点晚4s.已知各观测点到该中心的距离都是1020m.试确定该巨响发生的位置。(假定当时声音传播的速度为340m/s;相关各点均在同一平面上)
(19)(本小题满分10分)
已知抛物线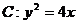 ,顶点为O,动直线
,顶点为O,动直线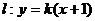 与抛物线
与抛物线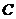 交于
交于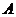 、
、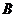 两点
两点
(I)求证: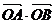 是一个与
是一个与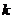 无关的常数;
无关的常数;
(II)求满足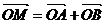 的点
的点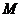 的轨迹方程。
的轨迹方程。
(20)(本小题满分12分)
已知向量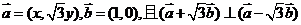 .
.
(Ⅰ)求点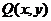 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)设曲线C与直线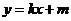 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点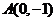 ,当
,当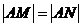 时,求实数
时,求实数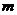 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com