
题目列表(包括答案和解析)
8.数列{an}中,a1=1,Sn是前n项和,当n≥2 时,an=3Sn,则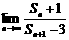 的值是
的值是
A.-2 B.- C.- D.1
7.设数列{an}是公比为a(a≠1),首项为b的等比数列,Sn是前n项和,对任意的n∈N+ ,点(Sn ,Sn+1)在
A.直线y=ax-b上 B.直线y=bx+a上
C.直线y=bx-a上 D.直线y=ax+b上
6.已知数列{an}的通项公式an=log2,设其前n项和为Sn,则使Sn<-5成立的正整数n
A.有最小值63 B.有最大值63
C.有最小值31 D.有最大值31
5.设等差数列{an}的前n项的和为Sn,若a1>0,S4=S8,则当Sn取得最大值时,n的值为
A.5 B.6 C.7 D.8
4.已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)=
A.8 B.-8 C.±8 D.
3.在等比数列{an}中,S4=1,S8=3,则a17+a18+a19+a20的值是
A.14 B.16 C.18 D.20
2.设Sn是等差数列{an}的前n项和,已知S6=36,Sn=324,Sn-6=144,则n=
A.15 B.16 C.17 D.18
只有一项是符合题目要求的.
1.数列-1,,-,,…错误!未定义书签。的一个通项公式是
A.an=(-1)n B.an=(-1)n
C.an=(-1)n D.an=(-1)n
2、(陕西省西安铁一中2009届高三12月月考)如图,在直角坐标系 中,已知椭圆
中,已知椭圆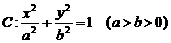 的离心率e=
的离心率e=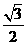 ,左右两个焦分别为
,左右两个焦分别为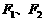 .过右焦点
.过右焦点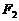 且与
且与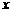 轴垂直的直线与椭圆
轴垂直的直线与椭圆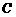 相交M、N两点,且|MN|=1 .
相交M、N两点,且|MN|=1 .
(Ⅰ) 求椭圆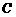 的方程;
的方程;
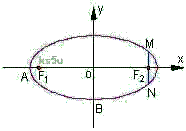 (Ⅱ) 设椭圆
(Ⅱ) 设椭圆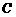 的左顶点为A,下顶点为B,动点P满足
的左顶点为A,下顶点为B,动点P满足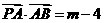 ,(
,(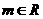 )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆
)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆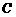 上.
上. 
解:(Ⅰ)∵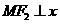 轴,∴
轴,∴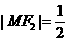 ,由椭圆的定义得:
,由椭圆的定义得: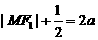 (2分)
(2分)
∵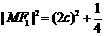 ,∴
,∴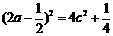 ,
(4分)
,
(4分)
又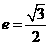 得
得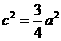 ∴
∴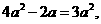
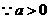
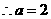
∴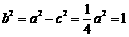 ,
(6分)
,
(6分)
∴所求椭圆C的方程为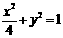 .
(7分)
.
(7分)
(Ⅱ)由(Ⅰ)知点A(-2,0),点B为(0,-1),设点P的坐标为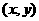
则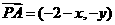 ,
,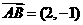 ,
,
由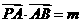 -4得-
-4得-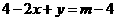 ,
,
∴点P的轨迹方程为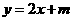 .
(9分)
.
(9分)
设点B关于P的轨迹的对称点为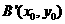 ,则由轴对称的性质可得:
,则由轴对称的性质可得:
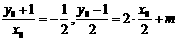 ,解得:
,解得: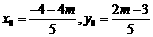 ,
(12分)
,
(12分)
∵点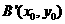 在椭圆上,∴
在椭圆上,∴
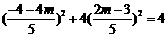 ,
,
整理得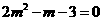 解得
解得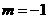 或
或
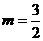
∴点P的轨迹方程为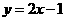 或
或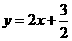 ,
(14分)
,
(14分)
经检验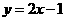 和
和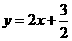 都符合题设,
都符合题设,
∴满足条件的点P的轨迹方程为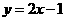 或
或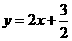 .
(15分)
.
(15分)
1、(山东省临沂高新区实验中学2008-2009学年高三12月月考)已知椭圆C过点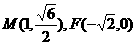 是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。
是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。
(1)求椭圆C的标准方程;
(2)求证:线段PQ的垂直平分线经过一个定点A;
(3)设点A关于原点O的对称点是B,求|PB|的最小值及相应点P的坐标。
解:(1)设椭圆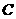 的方程为
的方程为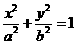 ,由已知,得
,由已知,得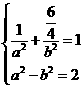 ,解得
,解得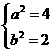
所以椭圆的标准方程为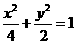 …………3分
…………3分
(2)证明:设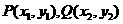 。由椭圆的标准方程为
。由椭圆的标准方程为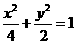 ,可知
,可知
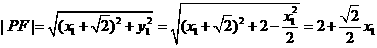
同理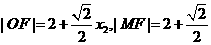 ………4分
………4分
∵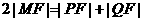 ,∴
,∴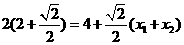
∴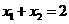 …………5分
…………5分
①当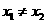 时,由
时,由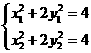 ,得
,得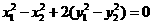
从而有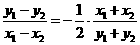
设线段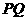 的中点为
的中点为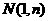 ,由
,由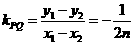 …………6分
…………6分
得线段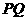 的中垂线方程为
的中垂线方程为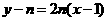 …………7分
…………7分
∴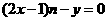 ,该直线恒过一定点
,该直线恒过一定点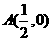 …………8分
…………8分
②当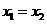 时,
时,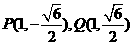 或
或 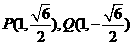
线段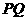 的中垂线是
的中垂线是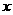 轴,也过点
轴,也过点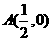 ,
,
∴线段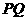 的中垂线过点
的中垂线过点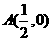 …………10分
…………10分
(3)由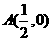 ,得
,得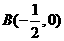 。
。
又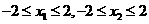 ,∴
,∴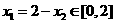
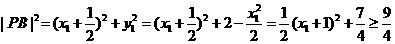 …………12分
…………12分
∴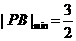 时,点
时,点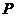 的坐标为
的坐标为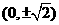 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com