
题目列表(包括答案和解析)
1.定义:⑴椭圆: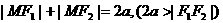 ;
;
⑵双曲线: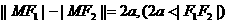 ;⑶抛物线:|MF|=d
;⑶抛物线:|MF|=d
8、直线与圆相交所得弦长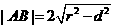
7.点、直线与圆的位置关系:(主要掌握几何法)
⑴点与圆的位置关系:(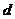 表示点到圆心的距离)
表示点到圆心的距离)
①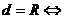 点在圆上;②
点在圆上;②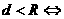 点在圆内;③
点在圆内;③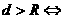 点在圆外。
点在圆外。
⑵直线与圆的位置关系:(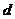 表示圆心到直线的距离)
表示圆心到直线的距离)
①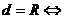 相切;②
相切;②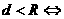 相交;③
相交;③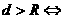 相离。
相离。
⑶圆与圆的位置关系:(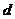 表示圆心距,
表示圆心距,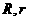 表示两圆半径,且
表示两圆半径,且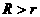 )
)
①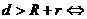 相离;②
相离;②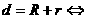 外切;③
外切;③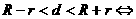 相交;
相交;
④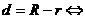 内切;⑤
内切;⑤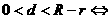 内含。
内含。
6.圆的方程的求法:⑴待定系数法;⑵几何法。
5.圆的方程:
⑴标准方程:①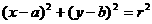 ;②
;②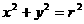 。
。
⑵一般方程: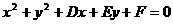 (
(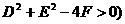
注:Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆 A=C≠0且B=0且D2+E2-4AF>0;
A=C≠0且B=0且D2+E2-4AF>0;
4.几个公式
⑴设A(x1,y1)、B(x2,y2)、C(x3,y3),⊿ABC的重心G:(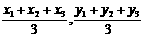 );
);
⑵点P(x0,y0)到直线Ax+By+C=0的距离: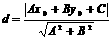 ;
;
⑶两条平行线Ax+By+C1=0与 Ax+By+C2=0的距离是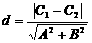 ;
;
3.两条直线的位置关系:
直线方程 平行的充要条件 垂直的充要条件 备注
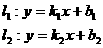
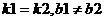
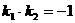
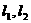 有斜率
有斜率
已知l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则l1 ⊥l2的充要条件是A1A2+B1B2=0。
2.求解线性规划问题的步骤是:
(1)列约束条件;(2)作可行域,写目标函数;(3)确定目标函数的最优解。
1.直线方程
⑴点斜式: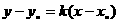 ;⑵斜截式:
;⑵斜截式: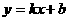 ;⑶截距式:
;⑶截距式: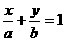 ;
;
⑷两点式: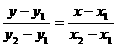 ;⑸一般式:
;⑸一般式: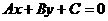 ,(A,B不全为0)。
,(A,B不全为0)。
6.结论:
⑴长方体从一个顶点出发的三条棱长分别为a,b,c,则对角线长为 ,全面积为2ab+2bc+2ca,体积V=abc。
,全面积为2ab+2bc+2ca,体积V=abc。
⑵正方体的棱长为a,则对角线长为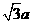 ,全面积为6a2,体积V=a3。
,全面积为6a2,体积V=a3。
⑶长方体或正方体的外接球直径2R等于长方体或正方体的对角线长。
⑷正四面体的性质:设棱长为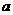 ,则正四面体的:
,则正四面体的:
高: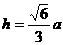 ;②对棱间距离:
;②对棱间距离: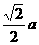 ;③内切球半径:
;③内切球半径: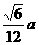 ;④外接球半径:
;④外接球半径: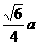 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com