6．(2009·潍坊模拟)函数f(x)＝x³+ax²+bx+a²在x＝1处有极值10，则　　　　　　　　　 (　)

A．a＝－11，b＝4　 　　　　　　　　　　　　　　　　　 B．a＝－4，b＝11

C．a＝11，b＝－4 　　　　　　　　　　　　　　　　　　 D．a＝4，b＝－11

解析　由f(x)＝x³+ax²+bx+a²，

得f′(x)＝3x²+2ax+b，

根据已知条件即

解得或(经检验应舍去)

答案　D

5．(2009·济宁联考)若函数f(x)＝x³－6bx+3b在(0,1)内有极小值，则实数b的取值范围是(　)

A．(0,1)　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．(－∞，1)

C．(0，+∞)　 　　　　　　　　　　　　　　　　　　　　　 D.

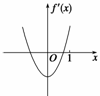解析　∵f′(x)=3x²-6b，由题意，函数f′(x)图象如右．

∴

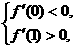
即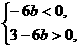得0<b<.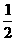

答案　D

4．(2008·湖北理，7)若f(x)＝－x²+bln(x+2)在(－1，+∞)上是减函数，则b的取值范围是

(　)

A．[－1，+∞)　 　　　　　　　　　　　　　　　　　　　 B．(－1，+∞)

C．(－∞，－1] 　　　　　　　　　　　　　　　　　　　　 D．(－∞，－1)

解析　由题意知f′(x)＝－x+≤0，x∈(－1，+∞)，

即f′(x)＝≤0，

即－x²－2x+b＝－(x+1)²+1+b≤0.

∴1+b≤0，b≤－1.

答案　C

3.(2008·福建文，11)如果函数y=f(x)的图象如图所示，那么导函数

y=f′(x)的图象可能是(　)

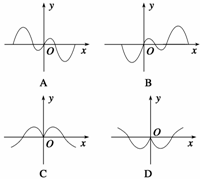
解析　由y＝f(x)的图象可知其单调性从左向右依次为增减增减，所以其导数y＝f′(x)的函数值依次为正负正负．由此可排除B、C、D.

答案　A

2．(2010·福州模拟)已知f(x)＝2x³－6x²+m (m为常数)在[－2,2]上有最大值3，那么此函数在[－2,2]上的最小值是　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－37　 　　　　　　　 B．－29 　　　　　　　　　　 　C．－5　 　　　　　　　　　 D．以上都不对

解析　∵f′(x)＝6x²－12x＝6x(x－2)，

∵f(x)在(－2,0)上为增函数，在(0,2)上为减函数，

∴当x＝0时，f(x)＝m最大．∴m＝3，从而f(－2)＝－37，f(2)＝－5.∴最小值为－37.

答案　A

1．(2010·聊城模拟)函数y＝x³－2ax+a在(0,1)内有极小值，则实数a的取值范围是(　)

A．(0,3)　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．(0，+∞)　 　　　　　　　　　　　　　　　　　　　　　 D．(－∞，3)

解析　令y′＝3x²－2a＝0，得x＝± (a>0，否则函数y为单调增函数)．若函数y＝x³－2ax+a在(0,1)内有极小值，则 <1，∴0<a<.

答案　B

12．(14分)(2010·厦门模拟)设有抛物线C：y＝－x²+x－4，通过原点O作C的切线y＝kx，

使切点P在第一象限．

(1)求k的值；

(2)过点P作切线的垂线，求它与抛物线的另一个交点Q的坐标．

解　(1)设点P的坐标为(x₁，y₁)，则y₁＝kx₁.①

y₁＝－x+x₁－4.②

①代入②得x+x₁+4＝0.

∵P为切点，∴Δ＝²－16＝0，

得k＝或k＝.

当k＝时，x₁＝－2，y₁＝－17.

当k＝时，x₁＝2，y₁＝1.

∵P在第一象限，∴所求的斜率k＝.

(2)过P点作切线的垂线，其方程为y＝－2x+5.③

将③代入抛物线方程得x²－x+9＝0.

设Q点的坐标为(x₂，y₂)，则2x₂＝9，

∴x₂＝，y₂＝－4.

∴Q点的坐标为.

§3.2　导数的应用

11．(13分)(2010·绍兴月考)设t≠0，点P(t,0)是函数f(x)＝x³+ax与g(x)＝bx²+c的图象的一

个公共点，两函数的图象在点P处有相同的切线．试用t表示a，b，c.

解　因为函数f(x)，g(x)的图象都过点(t,0)，

所以f(t)＝0，即t³+at＝0.因为t≠0，所以a＝－t².

g(t)＝0，即bt²+c＝0，所以c＝ab.

又因为f(x)，g(x)在点(t,0)处有相同的切线，

所以f′(t)＝g′(t)．

而f′(x)＝3x²+a，g′(x)＝2bx，所以3t²+a＝2bt.

将a＝－t²代入上式得b＝t.因此c＝ab＝－t³.

故a＝－t²，b＝t，c＝－t³.

10．(13分)(2009·衡阳模拟)求曲线f(x)＝x³－3x²+2x过原点的切线方程．

解　f′(x)＝3x²－6x+2.设切线的斜率为k.

(1)当切点是原点时k＝f′(0)＝2，

所以所求曲线的切线方程为y＝2x.

(2)当切点不是原点时，设切点是(x₀，y₀)，

则有y₀＝x－3x+2x₀，k＝f′(x₀)＝3x－6x₀+2，①

又k＝＝x－3x₀+2，②

由①②得x₀＝，k＝＝－.

∴所求曲线的切线方程为y＝－x.

9．(2009·江苏，9)在平面直角坐标系xOy中，点P在曲线C：y＝x³－10x+3上，且在第二象限内，已知曲线C在点P处的切线斜率为2，则点P的坐标为________．

解析　设P(x₀，y₀)(x₀<0)，由题意知：y′|x＝x₀＝3x－10＝2，∴x＝4.∴x₀＝－2，∴y₀＝15.∴P点的坐标为(－2,15)．

答案　(－2,15)