
题目列表(包括答案和解析)
18.(I)解:由题意得: ,由
,由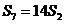 ,得
,得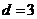
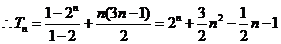
(II)解: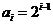 ,为1,2,4,8;
,为1,2,4,8;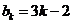 ,为1,4,7,10
,为1,4,7,10
有序实数对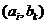 共有16个,
共有16个,
当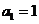 时,
时, 取1,4,7共3个;当
取1,4,7共3个;当 时,
时, 取1,4,7共3个
取1,4,7共3个
当 时,
时, 取1,4,7共3个;当
取1,4,7共3个;当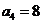 时,
时, 取1,4共2个;
取1,4共2个;
满足题意的点共11个,所求的概率为 .
.
18.已知数列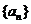 是等比数列,其首项
是等比数列,其首项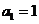 ,公比为2;数列
,公比为2;数列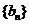 是等差数列,其首项
是等差数列,其首项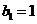 ,公差为
,公差为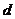 ,且其前
,且其前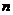 项的和
项的和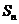 满足
满足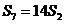 ;(I)求数列
;(I)求数列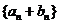 的前
的前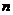 项
项
的和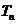 ;(II)在数列
;(II)在数列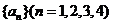 中任取一项
中任取一项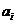 ,在数列
,在数列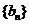
 中
中
任取一项 ,试求满足
,试求满足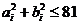 的概率.
的概率.
17.设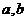 是异面直线,给出下列四个命题:①存在平面
是异面直线,给出下列四个命题:①存在平面 ,使
,使 ;
;
②存在惟一平面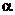 ,使
,使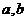 与
与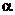 距离相等;③空间存在直线
距离相等;③空间存在直线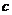 ,使
,使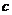 上任一点到
上任一点到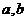 距离相等;④夹在异面直线
距离相等;④夹在异面直线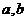 间的三条异面线段的中点不能共线。
间的三条异面线段的中点不能共线。
 其中正确命题的序号是 ①②③ 。
其中正确命题的序号是 ①②③ 。
16.已知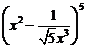 的展开式中的常数项为
的展开式中的常数项为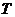 ,
, 是以
是以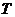 为周期的偶函数,且当
为周期的偶函数,且当
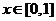 时,
时,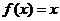 ,若在区间
,若在区间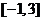 内,函数
内,函数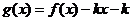 有4个零点,则实数
有4个零点,则实数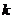 的取值范围是
的取值范围是 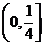 .
.
15.若直线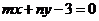 与圆
与圆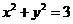 没有公共点,则以
没有公共点,则以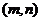 为点
为点 的坐标,过点
的坐标,过点
 的一条直线与椭圆
的一条直线与椭圆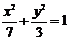 的公共点有
2 个.
的公共点有
2 个.
14.当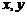 满足约束条件
满足约束条件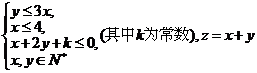 的最大值为12,则
的最大值为12,则 的
的
取值范围是 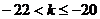 .
.
13.已知空间三个平面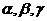 两两垂直,直线
两两垂直,直线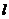 与平面
与平面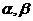 所成的角都是
所成的角都是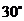 ,则直线
,则直线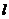 与
与
平面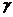 所成的角是______
所成的角是______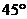 ___
.
___
.
12.过圆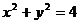 外一点P(2,4)作圆的切线,切点为A、B,则△APB的外接圆
方程为
外一点P(2,4)作圆的切线,切点为A、B,则△APB的外接圆
方程为  .
.
11.从装有3个红球,2个白球的袋中随机取出2个球,以 表示取得红球的个数,则
表示取得红球的个数,则 0.6
,
0.6
,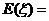 1.2 .
1.2 .
10.函数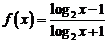 ,若
,若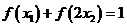 (其中
(其中 、
、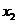 均大于2),则
均大于2),则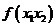
的最小值为 A. B.
B.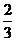 C.
C. D.
D. (B)
(B)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com