
题目列表(包括答案和解析)
(11)若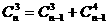 , 则n的值为
.
, 则n的值为
.
(12) 一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 .
(13) 若10把钥匙中只有2把能打开某锁,则从中任取2把能将该锁打开的概率为 ..
(14) 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,则这对双胞胎的作业同时被抽中的概率是 (结果用最简分数表示).
(1) 从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲、乙两人不去巴黎游览,则则不同的选择方案 ( )
A.300种 B.240种 C.144种 D.96种
(2) 北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作,若每天早、中、晚三班,每4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
A.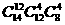 B.
B.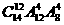 C.
C.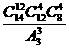 D.
D.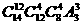
(3) 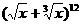 的展开式中,含x的正整数次幂的项共有 ( )
的展开式中,含x的正整数次幂的项共有 ( )
A.4项 B.3项 C.2项 D.1项
(4)某班新年联欢会原定的5个节目已排成节目单, 开演前又增加了两个新节目. 如果将这两个新节目插入原节目单中, 那么不同插法的种数为 ( )
A.42 B. 96 C. 48 D. 124
(5) 设直线的方程是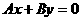 ,从1,2,3,4,5这五个数中每次取两个不同的数作为A、B的值,则所得不同直线的条数是 ( )
,从1,2,3,4,5这五个数中每次取两个不同的数作为A、B的值,则所得不同直线的条数是 ( )
A.20 B.19 C.18 D.16
(6)从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( )
A. 140种 B. 120种 C. 35种 D. 34种
(7) 四棱锥的八条棱代表8种不同的化工产品,由公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共点的两条棱代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为 ( )
A.96 B.48 C.24 D.0
(8) 将9个(含甲、乙)平均分成三组,甲、乙分在同一组,则不同分组方法的种数为( )
A.70 B.140 C.280 D.840
(9)四面体的顶点和各棱中点共10个点, 在其中取4个不共面的点, 则不同的取法共有( )
A. 150种 B. 147种 C. 144种 D. 141种
(10) 从数字1,2,3,4,5中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为 ( )
A. 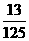 B.
B. 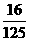 C.
C. 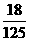 D.
D. 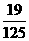
18、某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞ 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
17、某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数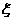 的分布列和
的分布列和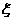 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
16、甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所出次品数分别为ξ 、η,且ξ和η的分布列为:
|
ξ |
0 |
1 |
2 |
|
P |
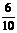 |
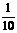 |
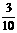 |
试比较这两名工人谁的技术水平更高.
15、从4名男生和2名女生中任选3人参加演讲比赛,设随机变量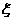 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求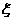 的分布列;
的分布列;
(Ⅱ)求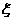 的数学期望;
的数学期望;
(Ⅲ)求“所选3人中女生人数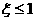 ”的概率.
”的概率.
|
η |
0 |
1 |
2 |
|
P |
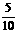 |
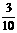 |
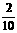 |
14、某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%,一旦失败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
|
投资成功 |
投资失败 |
|
192次 |
8次 |
则该公司一年后估计可获收益的期望是___________(元)..
13、一个容量为n的样本,分成若干组,已知某组频数和频率分别为36和0.25,则n=__________.
12、一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个球,则其中含红球个数的数学期望是 .
11、随机变量ξ的分布列为P(ξ=k)=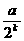 (k=0,1,2,…,10)则
(k=0,1,2,…,10)则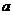 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com