8．从甲地到乙地有A₁、A₂、A₃共3条路线，从乙地到丙地有B₁、B₂共2条路线，其中A₂B₁是从甲地到丙地的最短路线，某人任选了1条从甲地到丙地的路线，它正好是最短路线的概率为_______．

7．已知某厂产品的次品率为0.5%，则该厂18000件产品中合格品的件数可能为_____件．

6．下列说法：

①频率是反映事件发生的频繁程度，概率反映事件发生的可能性的大小　②做n次随机试验，事件A发生m次，则事件A发生的概率为　③频率是不能脱离n次试验的实验值，而概率是具有确定性的不依赖于试验次数的理论值　④频率是概率的近似值，概率是频率的稳定值

其中正确命题的序号为________________．

5．下列说法中正确的是(　)

A．设有一批产品，其次品率为0.05，则从中任取200件，必有10件次品

B．做100次抛硬币的试验，有51次出现正面．因此出现正面的概率是0.51

C．随机事件A的概率是频率的稳定值，频率是概率的近似值

D．若事件A发生的概率趋近于0，则事件A是不可能事件

4．12本外形相同的书中，有10本语文书，2本数学书，从中任意抽取3本书，则必然事件为(　)

A．3本都是语文书　 B．至少有一本是数学书

C．3本都是数学书　 D．至少有一本是语文书

3．若在同等条件下进行n次重复试验得到某个事件A发生的频率f(n)，则随着n的逐渐增加，有(　)

A．f(n)与某个常数相等

B．f(n)与某个常数的差逐渐减小

C．f(n)与某个常数差的绝对值逐渐减小

D．f(n)在某个常数附近摆动并趋于稳定

2．随机事件A的频率满足(　)

A.＝0　 　　　　B.＝1 　　　C.＞1 　　　D．0≤≤1

1.将一枚硬币向上抛掷10次，其中正面向上恰有5次是(　)

A．必然事件　B．随机事件　C．不可能事件　D．无法确定

20.(本小题满分14分)已知m∈R，设P：x₁和x₂是方程x²－ax－2＝0的两个根，不等式|m－5|≤|x₁－x₂|对任意实数a∈[1,2]恒成立；Q：函数f(x)＝3x²+2mx+m+有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.

解：由题设x₁+x₂＝a，x₁x₂＝－2，

∴|x₁－x₂|＝＝.

当a∈[1,2]时，的最小值为3.

要使|m－5|≤|x₁－x₂|对任意实数a∈[1,2]恒成立，只须|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x²+2mx+m+＝0的判别式

Δ＝4m²－12(m+)＝4m²－12m－16>0，

得m<－1或m>4.

综上，要使“P∧Q”为真命题，只需P真Q真，即

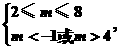
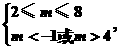
解得实数m的取值范围是(4,8].

19.(本小题满分14分)设全集I＝R已知集合M＝{x|(x+3)²≤0}，N＝{x|2x²＝()}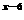

(1)求(∁_IM)∩N

(2)记集合A＝(∁_IM)∩N，已知B＝{x|a－1≤x≤5－a，a∈R}，若B∪A＝A.求实数a的取值范围.

解：(1)∵M＝{x|(x+3)²≤0}＝{－3}，

N＝{x|2x²＝2^6－x}＝{x|x²+x－6＝0}＝{－3,2}，

∴∁_IM＝{x|x∈R且x≠－3}，

∴(∁_IM)∩N＝{2}.

(2)A＝(∁_IM)∩N＝{2}，

∵A∪B＝A，∴B⊆A，

∴B＝∅或B＝{2}.

当B＝∅时，a－1>5－a，

∴a>3；

当B={2}时,.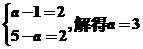

综上所述，所求a的取值范围为{a|a≥3}.