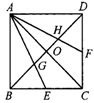
2．如图2所示，四边形ABCD为一正方形，E、F分别为BC、CD的中点，对角线AC与BD相交于O点，且AE与OB相交于G点，AF与OD相交于H点，下列说法正确的有(　 )

　　 ①E点是线段BC的重心;②G点是△ABC的重心;

　　 ③H点是△ADC的重心;④O点是正方形ABCD的重心.

　　 A．1个　　 B．2个　　　 C．3个　　　 D．4个

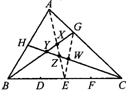
1．如图1所示，△ABC，D、E、F三点将BC四等分，AG：AC=1：3，H为AB的中点，下列哪一个点为△ABC的重心(　 )

A．X　　　 B．Y　　　 C．Z　　　 D．W

　　　　　　 (1)　　　　　　　　　　　　 (2)　　　　　　　　　　　 (3)

6．已知3(a²+b²+c²)=(a+b+c)²，求证：a=b=c．

本资料由《七彩教育网》 提供！

5．写出下列命题的逆命题，并指出其真假．

　(1)若a=b，则(a-b)² =0；

　(2)若a=b，则a²-b²=0；

　(3)若a≠b，则a²+b²＞2ab；

3．有某种产品100个，通过两种检查，第一种检查合格品有90个，第二种检查合格品有78个，两种检查都合格的有72个．试问这100个产品中，通过两种检查都不合格的产品有多少个？

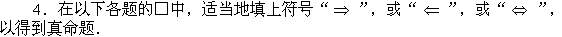
　(1)a＞0□│a│＞0；

　(2)a＝0且b=0□a²+b²=0；

　(3)(x-a)(x-b)=0□x=a或x=b；

　(4)如果α＞1，β＞2，γ＞3，那么，α□γ，β□α，β□γ．

1．已知A={1，2，3，4，5}，B={1，3，5，7}，C={2，3，5，8} ，写出集合：

　(1)A∩B∩C； (2)A∪B∪C；

　(3)A∩(B∪C)；(4)A∪(B∩C)．

2．命题和证明

　(1)命题和逆命题

　人们在思维活动中，经常要对客观事物做出判断．例如：

　(i)雪是白的；

　(ii)如果∠1和∠2是对顶角，那么∠1=∠2；

　(iii)3+4=6；

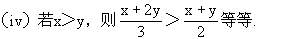
　上述所列都是对客观事物做出判断的语句．人们对客观事物的情况做出判断可能是正确的(真)，也可能是错误的(假)．我们把肯定或否定的判断语句叫作命题．上述语句(i)，(ii)，(iii)，(iv)都是命题．

　关于命题的真假性，有些容易判断，如(i)，(ii)是真命题，(iii)是假命题．但对(iv)的真假性就不是显然可判断的．可通过设x=1，y=0(x＞y)，那么

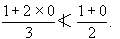
　因此，命题(iv)为假命题(注意：证明一个命题为真命题，必须通过逻辑推演，但要证明一个命题为假命题只须举出一个反例即可)．

　数学命题具有多种形式，经常采用的命题形式是“若α，则β”，“如果α，那么β”．

　命题“若α，则β”或是真命题，或是假命题，二者必居其一．“若

　当由α不可能推出β时，“若α，则β”便是假命题．

　在命题“若α，则β”中，α叫作这个命题的条件，β叫作这个命题的结论．如果将命题“若α，则β”的条件和结论互换，就得到一个新命题“若β，则α”，这两个命题之间具有互连关系，其中一个叫作原命题时，则另一个命题就叫作这个原命题的逆命题．

　当“如果α，则β”为真命题时，它的逆命题“如果β，则α”不一定是真命题．例如：

　(i)“如果2×3=6，那么6÷3=2”是真命题．它的逆命题“如果6÷3=2，那么2×3=6”也是真命题．

　(ii)“若a=0并且b=0，则ab=0”是真命题，但它的逆命题“若ab=0，则a=0并且b=0”就不是真命题．

　(iii)“如果∠1，∠2是对顶角，那么∠1=∠2”是真命题，但它的逆命题“∠1=∠2，那么∠1，∠2是对顶角”就是假命题．

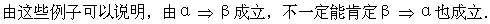
　(2)证明

　我们要说明“若α，则β”是真命题时，以什么方式来推证呢？最常用的基本格式就是推出关系的传递性，即：

　如果

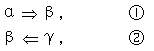
　那么

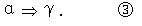
　例如，(i)若

　∠1和∠2是对顶角，①

　对顶角相等，②

　则 ∠1=∠2．③

　(ii) 张三是人，①

　凡人必有死，②

　所以张三必有死．③

　上述推理格式叫作三段论式，推理中的①，②是两个前提条件，①叫小前提，②叫大前提，③是由①，②推出的结论．

　实际上，三段论式和推出关系的传递性是一致的．例如“对顶角相等”的证明过程，可以像下面这样来理解．

　已知：∠1是∠2的对顶角(图2-98)，求证：∠1=∠2．

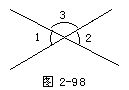
　证

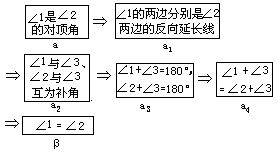
　从上述证明过程可知，要证明“若α，则β”，我们先设法找出一

　应用已经被确认的正确命题和已知条件作根据，经过推演，导出某一命题成立，这种方法就叫作演绎推理法(简称演绎法)．演绎法是证明数学问题的重要方法．

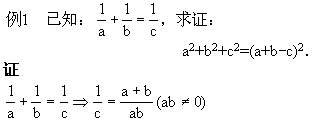
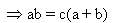
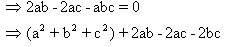
　　　＝a²+b²+c²

　(a+b-c)²=a²+b²+c².

　例2 某校数学竞赛，A，B，C，D，E，F，G，H八位同学获得了前八名，老师叫他们猜一下谁是第一名．A说：“或者F，或者H是第一名．”B说：“我是第一名．”C说：“G是第一名．”D说：“B不是第一名．”E说：“A说的不对．”F说：“我不是第一名．”G说：“C不是第一名．”H说：“我同意A的意见．”老师说八个人中有三人猜对了，那么试问第一名是谁？

　分解与解 由已知条件可知：A与H同真假，E与F同真假，B与D必定一真一假．

　(i)如果A与H猜对了，那么D与G也都猜对了．这样就有四人猜对，不合题意，因此，A与H必定都猜错了．

　(ii)如果E与F猜对了，即F与H都不是第一名，这时若B猜对了，那么D就猜错了，C也猜错了，G猜对了，这样，就有E，F，B，G四人猜对，也与题意不符．因此B猜的不对，D猜对了，这时已有E，F，D三人猜对，所以G，C都必定猜错了，所以C是第一名．

练习十七

1．推出关系

　如果设A={x│x是4的倍数}，B={x│x是2的倍数}，则A中元素具有性质α--4的倍数；B中元素具有性质β--2的倍数．我们知道：如果某元素x是4的倍数，那么x一定是2的倍数，即具有性质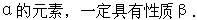

　一般地说，如果具有性质α的元素也具有性质β，我们便说由α推

　下面再举一个例子．

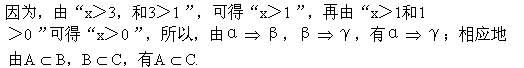
2．集合之间的关系和运算

　(1)包含与子集

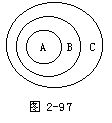
　(i)你班上的同学的集合和你学校的同学的集合之间的关系是：前者是后者的子集，后者包含前者．

　(ii)设集合

　例1 设A={1，2，3，4}，试写出A的所有子集．

　{1，3}，{1，4}，{2，3}，{2，4}，{3，4}，{1，2，3}，{1，2，4}，{2，3，4}，{1，3，4}，{1，2，3，4}．

　(2)交集运算

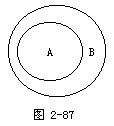
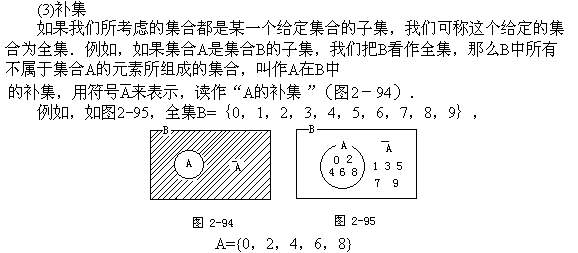
　对于给定的集合A，B，由它们的公共元素所构成的集合叫作集合A与B的交集．我们用A∩B表示A，B的交集(图2-88)．例如

　(i)如图2-89，设

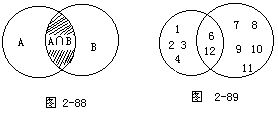
A={x│x是12的正因数}，

B={x│5＜x＜13，x是整数}，

　则

　A={1，2，3，4，6，12}，B={6，7，8，9，10，11，12}．

　所以 A∩B={6，12}．

　(ii)设l₁，l₂是平面上两条不同的直线，则l₁∩l₂就是由它们的交点组成的集合．

　如果l₁与l₂相交于一点P，则l₁∩l₂={P}(图2-90)；

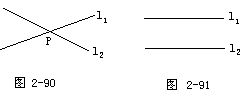
　(3)并集运算

　对于给定的两个集合A，B，把它们所含的元素合并起来所构成的集合，叫作集合A，B的并集，我们用符号A∪B表示A，B的并集(图2-92)．例如

　(i)设M，N分别表示你班上男生、女生的集合，那么M∪N就是你班上同学的集合．

　(ii)设

A={1，3，5，7，9}，B={2，3，4，5，6}，

　则 A∪B={1，2，3，4，5，6，7，9}．

　注意 在求上述集合A，B的并集时，虽然在A，B中都有3和5，但在A∪B中，3，5只取一次．

　(iii)设E={x│x是实数，且x≥4}，

　F={x│x是实数，且x≤-4}，G={x│x²≥16}．

　则 E∪F=G．

　一般地说，如果α，β分别是集合A，B的特征性质，即

　A={x│x具有性质α} ，B={x│x具有性质β}，则A∪B就是那些具有性质α或性质β的元素组成的集合，也就是

A∪B={x│x具有性质α或β}，

　或者

A∪B={x│x∈A或x∈B}．

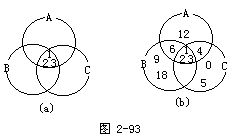
　例2 设

　A={x│x是12的正因数}，B={x│x是18的正因数}，

C={x│0≤x≤5，且x∈Z}．

　求：(1)A∩B∩C；(2)A∪B∪C．

　解 根据已知条件，用填文氏图各区域的元素的方法来解决(如图2-93(a)，(b)).

　(1)A∩B∩C={1，2，3}；

　(2)A∪B∪C={0，1，2，3，4，5，6，9，12，18}．

　例3 设A={1，a，a²} ，B={1，a，b)，假定A，B中的元素都是整数，并且A∩B={1，3}，A∪B={1，a，2a，3a}，求a，b的值．

　解 因为A={1，a，a²}，B={1，a，b}，所以

A∩B＝{1，a}．

　已知A∩B={1，3}．所以a=3．又由于

　A∪B={1，a，b，a²}={1，a，2a，3a}={1，3，6，9}，所以b=6．

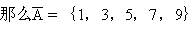
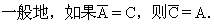
§17．2简易逻辑

　逻辑一词是LOGIC的音译，它是研究思维法则的一门学科．数学和逻辑的关系非常密切，在此，对逻辑知识做一些初步介绍．

1．集合的描述方法

　(1)列举法

　当一个集合所含元素个数较少时，一个最简单的描述方法就是把它所含的每个元素都列举出来，这叫列举法．用列举法表示集合，通常是将这个集合的每个元素一一填写在{}中，每个元素之间用逗点隔开．填写集合的元素时，与元素的排列次序无关．例如：

　(i)由a，b，c，d，e五个小写字母组成的集合A，记作

A={a，b，c，d，e}，

　也可记作

A={b，a，c，d，e)．

　(ii)由小于40的质数组成的集合B，记作

B={2，3，5，7，11，13，17，19，23，29，31，37}．

　(iii)平方等于1的有理数集合C，记作

C={1，-1}．

　(iv)三条直线l₁，l₂，l₃组成的集合D，记作

D={l1，l2，l3}．

　(2)特征性质描述法

　当一个集合所含元素较多时，用列举法描述很麻烦，这就要用到特征性质描述法．

　所谓特征性质是指集合中元素的特征性质，即：(i)这个集合中每个元素都具有这些性质；(ii)具有这些性质的事物都是这个集合的元素．

　例如，集合={1,-1}用特征性质描述法表示就是

A={x│x²=1}，

　或者

A={x││x│=1}．

　全体偶数组成的集合B，用特征性质描述法表示就是

B={x│x是能被2整除的整数}，

　或者

B={2n│n是整数}．

　全体奇数组成的集合C，用特征性质描述法表示就是

C={x│x是不能被2整除的整数}，

　或者

C={2n+1│n是整数}，

C={2n-1│n是整数}．

　一般地，用特征性质α表示集合A的形式是：

A={x│x具有性质α}．