
题目列表(包括答案和解析)
5.求证:对任意自然数n,n(n-1)(2n-1)能被6整除.
4.设p是大于3的质数,求证:24|(p2-1).
3.已知整数x,y,使得7|(13x+8y),求证:
7|(9x+5y).
2.证明:当a是奇数时,a(a2-1)能被24整除.
1.求证:对任意自然数n,2×7n+1能被3整除.
2.证明整除的基本方法
证明整除常用下列几种方法:(1)利用基本性质法;(2)分解因式法;(3)按模分类法;(4)反证法.下面举例说明.
例1 证明:三个连续奇数的平方和加1,能被12整除,但不能被24整除.
分析 要证明一个数能被12整除但不能被24整除,只需证明此数等于12乘上一个奇数即可.
证 设三个连续的奇数分别为2n-1,2n+1,2n+3(其中n是整数),于是
(2n-1)2+(2n+1)2+(2n+3)2+1
=12(n2+n+1).
所以
12|[(2n-1)2+(2n+1)2+(2n+3)2].
又n2+n+1=n(n+1)+1,而n,n+1是相邻的两个整数,必定一奇一偶,所以n(n+1)是偶数,从而n2+n+1是奇数,故
24 [(2n-1)2+(2n+1)2+(2n+3)2].
[(2n-1)2+(2n+1)2+(2n+3)2].
例2 若x,y为整数,且2x+3y,9x+5y之一能被17整除,那么另一个也能被17整除.
证 设u=2x+3y,v=9x+5y.若17|u,从上面两式中消去y,得
3v-5u=17x.①
所以 17|3v.
因为(17,3)=1,所以17|v,即17|9x+5y.
若17|v,同样从①式可知17|5u.因为(17,5)=1,所以17|u,即17|2x+3y.
 q>1.求pq的值.
q>1.求pq的值.
解 若p=q,则
不是整数,所以p≠q.不妨设p<q,于是
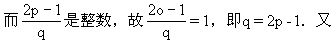
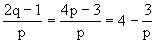
是整数,所以p只能为3,从而q=5.所以
pq=3×5=15.
例4 试求出两两互质的不同的三个自然数x,y,z,使得其中任意两个的和能被第三个数整除.
分析 题中有三个未知数,我们设法得到一些方程,然后从中解出这些未知数.
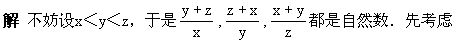 最小的一个:
最小的一个:
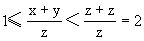
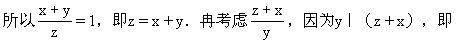
y|(y+2x),所以y|2x,于是
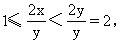
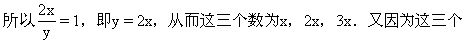 数两两互质,所以x=1.
数两两互质,所以x=1.
所求的三个数为1,2,3.
例5 设n是奇数,求证:
60|6n-3n-2n-1.
分析 因为60=22×3×5,22,3,5是两两互质的,所以由性质6,只需证明22,3,5能被6n-3n-2n-1整除即可.对于幂的形式,我们常常利用性质8-性质10,其本质是因式分解.
证 60=22×3×5.由于n是奇数,利用性质8和性质10,有
22|6n-2n,22|3n+1,
所以
22|6n-2n-3n-1, 3|6n-3n, 3|2n+1,
所以
3|6n-3n-2n-1,5|6n-1,5|3n+2n,
所以
5|6n-1-3n-2n.
由于22,3,5两两互质,所以
60|6n-3n-2n-1.
我们通常把整数分成奇数和偶数两类,即被2除余数为0的是偶数,余数为1的是奇数.偶数常用2k表示,奇数常用2k+1表示,其实这就是按模2分类.又如,一个整数a被3除时,余数只能是0,1,2这三种可能,因此,全体整数可以分为3k,3k+1,3k+2这三类形式,这是按模3分类.有时为了解题方便,还常把整数按模4、模5、模6、模8等分类,但这要具体问题具体处理.
例6 若整数a不被2和3整除,求证:24|(a2-1).
分析 因为a既不能被2整除,也不能被3整除,所以,按模2分类与按模3分类都是不合适的.较好的想法是按模6分类,把整数分成6k,6k+1,6k+2,6k+3,6k+4,6k+5这六类.由于6k,6k+2,6k+4是2的倍数,6k+3是3的倍数,所以a只能具有6k+1或6k+5的形式,有时候为了方便起见,也常把6k+5写成6k-1(它们除以6余数均为5).
证 因为a不被2和3整除,故a具有6k±1的形式,其中k是自然数,所以a2-1=(6k±1)2-1=36k2±12k=12k(3k±1).由于k与3k±1为一奇一偶(若k为奇数,则3k±1为偶数,若k为偶数,则3k±1为奇数),所以2|k(3k±1),于是便有24|(a2-1).
例7 求证:3n+1(n为正整数)能被2或22整除,但不能被2的更高次幂整除.
证 按模2分类.若n=2k为偶数,k为正整数,则
3n+1=32k+1=(3k)2+1.
由3k是奇数,(3k)2是奇数的平方,奇数的平方除以8余1,故可设(3k)2=8l+1,于是
3n+1=8l+2=2(4l+1).
4l+1是奇数,不含有2的因数,所以3n+1能被2整除,但不能被2的更高次幂整除.
若n=2k+1为奇数,k为非负整数,则
3n+1=32k+1+1=3·(3k)2+1
=3(8l+1)+1=4(6l+1).
由于6l+1是奇数,所以此时3n+1能被22整除,但不能被2的更高次幂整除.
在解决有些整除性问题时,直接证明较为困难,可以用反证法来证.
例8 已知a,b是整数,a2+b2能被3整除,求证:a和b都能被3整除.
证 用反证法.如果a,b不都能被3整除,那么有如下两种情况:
(1)a,b两数中恰有一个能被3整除,不妨设3|a,3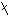 b.令a=3m,b=3n±1(m,n都是整数),于是
b.令a=3m,b=3n±1(m,n都是整数),于是
a2+b2=9m2+9n2±6n+1
=3(3m2+3n2±2n)+1,
不是3的倍数,矛盾.
(2)a,b两数都不能被3整除.令a=3m±1,b=3n±1,则
a2+b2=(3m±1)2+(3n±1)2
=9m2±6m+1+9n2±6n+1
=3(3m2+3n2±2m±2n)+2,
不能被3整除,矛盾.
由此可知,a,b都是3的倍数.
例9 设p是质数,证明:满足a2=pb2的正整数a,b不存在.
证 用反证法.假定存在正整数a,b,使得
a2=pb2
令(a,b)=d,a=a1d,b=b1d,则(a1,b1)=1.所以
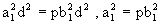

与(a1,b1)=1矛盾.
例10 设p,q均为自然数,且
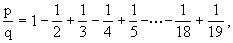
求证:29|p.
证 注意到29是质数.令a=10×11×…×19.
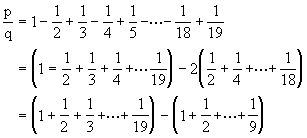
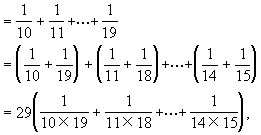
所以 ap=29q·b,
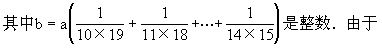
29|a·p,29是质数,且29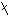 a,所以29|p.
a,所以29|p.
练习二十四
1.整除的基本概念与性质
所谓整除,就是一个整数被另一个整数除尽,其数学定义如下.
定义 设a,b是整数,b≠0.如果有一个整数q,使得a=bq,那么称a能被b整除,或称b整除a,并记作b|a.如果不存在这样的整数q,使得a=bq,则称a不能被b整除,或称b不整除a,记作b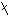 a.
a.
关于整数的整除,有如下一些基本性质:
性质1 若b|a,c|b,则c|a.
性质2 若c|a,c|b,则c|(a±b).
性质3 若c|a,c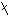 b,则c
b,则c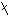 (a±b).
(a±b).
性质4 若b|a,d|c,则bd|ac.
性质5 若a=b+c,且m|a,m|b,则m|c.
性质6 若b|a,c|a,则[b,c]|a(此处[b,c]为b,c的最小公倍数).特别地,当(b,c)=1时,bc|a(此处(b,c)为b,c的最大公约数).
性质7 若c|ab,且(c,a)=1,则c|b.特别地,若p是质数,且p|ab,则p|a或p|b.
性质8 若a≠b,n是自然数,则(a-b)|(an-bn).
性质9 若a≠-b,n是正偶数,则(a+b)|(an-bn).
性质10 若a≠-b,n是正奇数,则(a+b)|(an+bn).
3.计算:
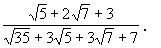
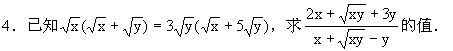
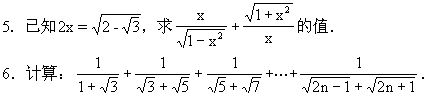
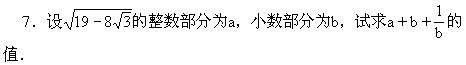
本资料由《七彩教育网》 提供!
2.计算:
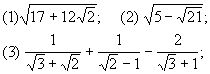
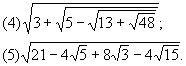
1.化简:
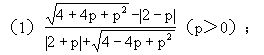
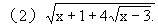
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com