
题目列表(包括答案和解析)
4.如图3,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:①AB=DE;②∠ABC=∠DEF;③∠ACB=∠DFE;④∠ABC+∠DFE=90°,其中成立的有( )
A.①②③④ B.①②③ C.①② D.②③
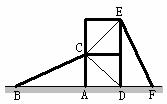
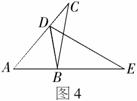
图3
*1.下列说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法为( )
A.①②③④ B.①③④ C.①②④ D.②③④
2.(2008年遵义市).如图,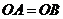 ,
,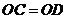 ,
,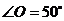 ,
,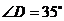 ,则
,则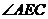 等于( )
等于( )
A.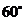 B.
B.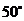 C.
C.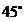 D.
D.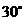
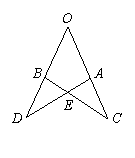
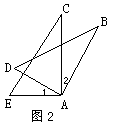
*3.如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C
C.∠D=∠E D.∠BAE=∠CAD
8.∵AB⊥CD,ED⊥BC,∴∠ABC=∠CDE=90°,在△ABC和△CDE中 ∴△ABC≌△CDE.∴∠A=∠ECD,∴∠ECD+∠ACB=90°,∴∠ACE=90°,∴AC⊥CE.
∴△ABC≌△CDE.∴∠A=∠ECD,∴∠ECD+∠ACB=90°,∴∠ACE=90°,∴AC⊥CE.
7. 证明: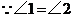 ,
,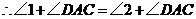 ,即:
,即: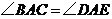
又在 和△ADE中
和△ADE中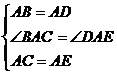 ,
, 
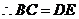
6.(1)证明: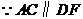 ,
,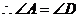 ,
,
在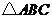 和
和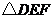 中
中
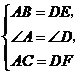

(2)答案不惟一,如: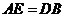 ,
, ,
,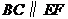 等.
等.
2.OB=OC;3.D;4.A,提示:本题暗含对顶角相等,故用“SAS”;5.∵AD∥BC,∴∠DAC=∠BCA
在△ADC和△CBA中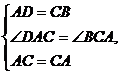 ∴△ADC≌△CBA. ∴∠BAC=∠DCA,∴AB∥CD.
∴△ADC≌△CBA. ∴∠BAC=∠DCA,∴AB∥CD.
1.D,提示:易证明△AOD≌△BOC而得AD=BC,∠C=∠D,由∠C=∠D得AD∥BC;
5.证明:连接DB,在△ADB和△CBD中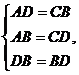 ∴△ADB≌△CBD(SSS)∴∠A=∠C.
∴△ADB≌△CBD(SSS)∴∠A=∠C.
第三课时答案:
4. ∵BE=CF,CE=CE,∴BC=EF,在△ABC和△DEF中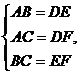
∴△ABC≌△DEF,(SSS)∴∠ACB=∠F,∴AC∥DF,∴∠EGC=∠D
1. SSS,提示:AD是公共边;2.AB=DC,提示:BC=CB是公共边;3.李明说法对.连接AD,则△ABD≌△ACD,所以∠B和∠C的大小发生变化,但∠B和∠C一直是相等的;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com