
题目列表(包括答案和解析)
(二)应用举例,深化巩固
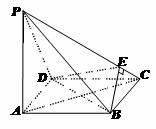
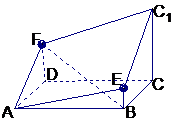
例1. 已知空间四边形ABCD中,P、Q分别是AB、CD的中点,且PQ=3,AC=4,BD=2 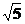 , AC与BD所成角的大小.
, AC与BD所成角的大小.
例2. 已知四面体ABCD的各棱长均相等,E、F分别为AB、CD的中点,求EF与AC所成角的大小.
例3. 在四面体ABCD中,平面ABD⊥平面BCD,△ABD为等边三角形,CD⊥BD,∠DBC=30o.
(1 )求二面角A-DC-B的大小; (2) 求二面角A-BC-D的平面角的正切值; (3) 求二面角D-AB-C的平面角的正切值.
解: 注意三垂线法的应用与讲解.
例4. 圆台上、下底面半径分别为2、4,O1A1、OB分别为上、下底面的半径,二面角A1-OO1-B是60o,圆台母线与底面成60o角. (1) 求A1B和OO1所成角的正切值; (2) 求圆台的侧面积及体积.
解; 注意 概念的转化, 实为一个三棱台的问题.
例5. 在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90o,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点,求CD与平面ADMN所成角的正弦.
解:注意到BN⊥面ADMN
第二章小结(4)-- 空间距离(08年7月10日)
(一)知识回顾,整体认识
1. 异面直线所成角;
2. 直线与平面所成角;
3. 两平面所成角.
27.如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1 求BF的长;
求BF的长;
解:(2注意到AE∥FC1)
28.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE。
29.(08高考 宁夏18)(本小题满分12分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图和侧视图在下面画出(单位:cm)(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(Ⅱ)按照给出的尺寸,求该多面体的体积;(Ⅲ)在所给直观图中连结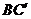 ,证明:
,证明: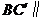 面
面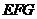 .
.


解:俯视图为:
第二章 小结(3)(08年7月9日)
(二)应用举例,深化巩固
1、如图,在三棱锥V-ABC中,VA=VC,AB=BC,求证:VB⊥AC.
2、过△ABC所在平面a外一点P, 作PO⊥a,垂足为O,连接PA,PB,PC.
(1)若PA=PB=PC,∠C=90°,则点O 是AB边的 中 点.
(2)若PA=PB=PC,则点O是△ABC的 外 心.
(3)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的 垂 心.
3、 如图,已知空间四边形ABCD的边BC=AC,AD=BD,引BE⊥CD,E为垂足,作AH⊥BE于H. 求证: AH⊥平面BCD.
如图,已知空间四边形ABCD的边BC=AC,AD=BD,引BE⊥CD,E为垂足,作AH⊥BE于H. 求证: AH⊥平面BCD.
4. 已知ABCD是正方形,PA⊥平面ABCD, BE⊥PC,E为垂足.
 求证:平面BDE⊥平面PBC.
求证:平面BDE⊥平面PBC.
解:PC⊥面BDE
训练提高练习: C组题:七、选择或填空题:
25、平面 平面
平面 ,平面
,平面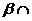 平面
平面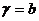 ,平面
,平面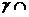 平面
平面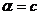 ,若
,若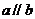 ,
,
则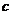 与
与 的位置关系是( D )
的位置关系是( D )
A.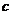 与
与 异面 B.
异面 B.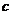 与
与 相交 C.
相交 C.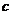 至少与
至少与 中的一条相交 D.
中的一条相交 D.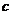 与
与 都平行
都平行
26.平面过直线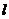 外的两点,若要这个平面与
外的两点,若要这个平面与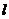 平行,则这样的平面有 ( D )
平行,则这样的平面有 ( D )
 A 无数个 B 一个 C不存在
D上述情况都有可能
A 无数个 B 一个 C不存在
D上述情况都有可能
(一)知识回顾,整体认识
1. 直线和平面垂直的判定及性质;
直线和平面垂直的判定及性质;
2. 平面和平面垂直的判定及性质.
22.正方体ABCD-A1B1C1D1 的棱长为
的棱长为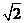 (1)、求△AB1D1的面积;(2)、求三棱锥
(1)、求△AB1D1的面积;(2)、求三棱锥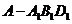 的体积。
的体积。
解、① ②
23.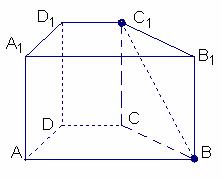 已知直四棱柱
已知直四棱柱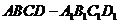 中,
中,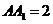 ,底面
,底面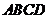 是直角梯形,
是直角梯形,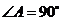 ,
,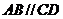 ,
,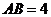 ,
,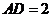 ,
,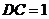 ,求异面直线
,求异面直线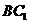 与
与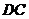 所成的角的余弦值
所成的角的余弦值 (解:为)
(解:为)
24、过正方体 的棱
的棱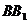 作一平面交平面
作一平面交平面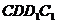 于
于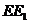 ,求证:
,求证: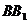 //
//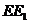
第二章 小结(2)(08年7月8日)
21.已知m、n是不同的直线,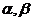 是不重合的平面,给出下列命题:①若
是不重合的平面,给出下列命题:①若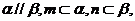 则
则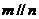 ②若
②若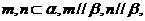 则
则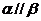
 ③m、n是两条异面直线,若
③m、n是两条异面直线,若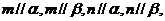 则
则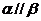
 上面命题中,真命题的序号是_____③_______(写出所有真命题的序号)
上面命题中,真命题的序号是_____③_______(写出所有真命题的序号)
20.连接抛物线上任意四点组成的四边形可能是 ②③⑤ (填写所有正确选项的序号) ①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形
①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形
19.三条直线中有两条平行,第三条和这两条都相交时确定 1 个平面;三条直线交于一点时可确定__1或者3 个平面;三条直线互相平行时,最多可确定 3 个平面。
18.三个平面将空间最少分成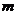 部分,最多分成
部分,最多分成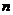 部分,则
部分,则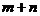 等于 12 .
等于 12 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com