练习册

  • 练习册
  • 试题

    题目列表(包括答案和解析)

     0  94162  94170  94176  94180  94186  94188  94192  94198  94200  94206  94212  94216  94218  94222  94228  94230  94236  94240  94242  94246  94248  94252  94254  94256  94257  94258  94260  94261  94262  94264  94266  94270  94272  94276  94278  94282  94288  94290  94296  94300  94302  94306  94312  94318  94320  94326  94330  94332  94338  94342  94348  94356  447348 

    14、在国民经济中，社会生产与货运之间有着密切的关系，下面列出1991年-2000年中某地区货运量y(亿吨)与工业总产值x(10亿元)的统计资料：

    年份
    		 1991
    		 1992
    		 1993
    		 1994
    		 1995
    x
    		 2、8
    		 2、9
    		 3、2
    		 3、2
    		 3、4
    y
    		 25
    		 27
    		 29
    		 32
    		 34
    年份
    		 1996
    		 1997
    		 1998
    		 1999
    		 2000
    x
    		 3、2
    		 3、3
    		 3、7
    		 3、9
    		 4、2
    y
    		 36
    		 35
    		 39
    		 42
    		 45

    利用上述资料：

    画出散点图；

    计算这两组变量的相关系数；

    在显著水平0、05的条件下，对变量x(10亿元)与y(亿吨)进行相关性检验；

    如果变量x(10亿元)与y(亿吨)之间具有线性相关关系，求出回归直线方程。

    试题详情

    13、随机选取15家销售公司，由营业报告中查出其上年度的广告费x(占总费用的百分比)及盈利额y(占销售总额的百分比)列表如下：

    x
    		 1.5
    		 0.8
    		 2.6
    		 1.0
    		 0.6
    		 2.8
    		 1.2
    		 0.9
    y
    		 3.1
    		 1.9
    		 4.2
    		 2.3
    		 1.6
    		 4.9
    		 2.8
    		 2.1
    x
    		 0.4
    		 1.3
    		 1.2
    		 2.0
    		 1.6
    		 1.8
    		 2.2
    		 　
    y
    		 1.4
    		 2.4
    		 2.4
    		 3.8
    		 3.0
    		 3.4
    		 4.0
    		 　

    试根据上述资料：

    画出散点图；

    计算出这两组变量的相关系数；

    在显著水平0、05的条件下，对变量x与y进行相关性检验；

    如果变量x与y之间具有线性相关关系，求出回归直线防城；

    已知某销售公司的广告费占其总费用的1、7%，试估计其盈利净额占销售总额的百分比。

    试题详情

    12、在钢丝线含碳量对于电阻的效应的研究中，得到如下的数据：

    含碳量x%
    		 0、10
    		 0、30
    		 0、40
    		 0、55
    电阻y
    		 15
    		 18
    		 19
    		 21
    含碳量x%
    		 0、70
    		 0、80
    		 0、95
    		 　
    电阻y
    		 22、6
    		 23、8
    		 26
    		 　

    (1)画出电阻y(20℃,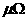)关于含碳量x的散点图；

    (2)求出y与x的相关系数；

    (3)求出电阻y关于含碳量x之间的回归直线方程。

    试题详情

    11、某种合金的抗拉强度y(kg/m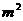)与其中的含碳量x(%)有关，今测得12对数据如下表所示：

    x
    		 0.10
    		 0.11
    		 0.12
    		 0.13
    		 0.14
    		 0.15
    y
    		 42.0
    		 43.5
    		 45.0
    		 45.5
    		 45.0
    		 47.5
    x
    		 0.16
    		 0.17
    		 0.18
    		 0.20
    		 0.21
    		 0.23
    y
    		 49.0
    		 53.0
    		 50.0
    		 55.0
    		 55.0
    		 60.0

    利用上述资料：

    作出抗拉强度y关于含碳量x的散点图；

    建立y关于x的一元线性回归方程。

    试题详情

    10、对于回归方程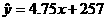，当x=28时，y的估计值是　　　　　　　 。

    试题详情

    9、相应于显著性水平0、05，观测值为10组的相关系数临界值为 　　　　　　　　　　　。

    试题详情

    8、　　　　　　　　　 叫做变量y与x之间的相关系数。

    试题详情

    7、回归直线方式：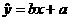

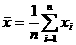
    相应的直线叫回归直线，对两个变量所进行的上述统计分析叫线性回归分析。

    试题详情

    6、有下列关系：① 人的年龄与他(她)拥有的财富之间的关系；② 曲线上的点与该点的坐标之间的关系；③ 苹果的产量与气候之间的关系；④ 森林中的同一种树木，其断面直径与高度之间的关系；⑤ 学生与他(她)的学号之间的关系、其中有相关关系的是　　　　　　　　　　　　 。

    试题详情

    5、若变量y与x之间的相关系数r=－0.9362，查表得到相关系数临界值r0.05=0.8013，则变量y与x之间(　 )

    A、不具有线性相关关系　　　　　　　 B、具有线性相关关系

    C、它们的线性关系还要进一步确定　　 D、不确定

    试题详情


    同步练习册答案