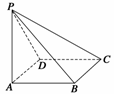
19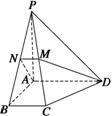．(10分)如图所示，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.

(1)求证：PB⊥DM；

(2)求BD与平面ADMN所成的角.　　　　　　　　

(1)证明　 ∵N是PB的中点，PA=AB，

∴AN⊥PB.∵∠BAD=90°，∴AD⊥AB.

∵PA⊥平面ABCD，∴PA⊥AD.

∵PA∩AB=A，∴AD⊥平面PAB，∴AD⊥PB.　　　　　　　

又∵AD∩AN=A，∴PB⊥平面ADMN.

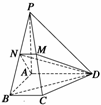∵DM平面ADMN，∴PB⊥DM.　　　　　　　　　　　　

(2)解　 连接DN，

∵PB⊥平面ADMN，

∴∠BDN是BD与平面ADMN所成的角，　　　　　　　　

在Rt△BDN中，

sin∠BDN===，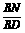　　　　　　　　　　　　　　

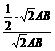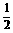∴∠BDN=30°,即BD与平面ADMN所成的角为30°.　　　　　　　　　　　

20(10分)．如图所示，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，

∠ABC=60°,E,F分别是BC,PC的中点.

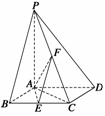(1)证明:AE⊥PD;

(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,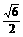

求二面角E-AF-C的余弦值.

(1)证明　 由四边形ABCD为菱形,∠ABC=60°,

可得△ABC为正三角形.因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.

因为PA⊥平面ABCD,AE平面ABCD,所以PA⊥AE.

而PA平面PAD,AD平面PAD且PA∩AD=A,

所以AE⊥平面PAD.又PD平面PAD,所以AE⊥PD.

(2)解　 如图所示，设AB=2,H为PD上任意一点,连结AH、EH,

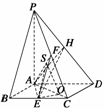由(1)知,AE⊥平面PAD,

则∠EHA为EH与平面PAD所成的角.

在Rt△EAH中,AE=,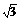

所以,当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大.

此时,tan∠EHA=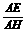==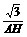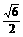,因此AH=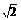.又AD=2,所以∠ADH=45°,所以PA=2.

方法一　 因为PA⊥平面ABCD,PA平面PAC,

所以,平面PAC⊥平面ABCD.过E作EO⊥AC于O,则EO⊥平面PAC,

过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角.

在Rt△AOE中,EO=AE·sin30°=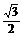,AO=AE·cos30°=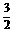,又F是PC的中点,

在Rt△ASO中,SO=AO·sin45°=,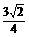

又SE===,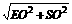

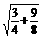在Rt△ESO中,cos∠ESO===,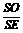

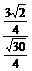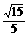即所求二面角的余弦值为.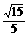

18．(9分)如图所示三棱锥P-ABC中，异面直线PA与BC所成的角为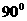，二面角P-BC-A为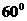，△PBC和△ABC的面积分别为16和10，BC＝4. 求：

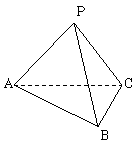(1)PA的长；(2)三棱锥P-ABC的体积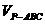

(1)作AD⊥BC于D，连PD，由已知PA⊥BC，∴BC⊥面PAD，∴BC⊥PD，∴∠PDA为二面角

的平面角，∴∠PDF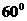＝，可算出PD＝8，AD＝5，∴PA＝7;(2)V＝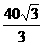

17.(8分)在正四面体P-ABC中,D,E,F分别是AB 、BC、 CA的中点,求证:

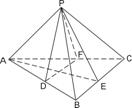(1)BC∥平面PDF;　 (2)BC⊥平面PAE

略

16．(8分)已知A(3,1),B(0,-1),C(1,3), D(a,b),则当a,b满足什么条件时,可以使得

　　 (1)AB∥CD; (2)AB⊥CD.

略

15.已知△ABC的三个顶点的坐标分别为A(0,3),B(4,1),C(3,4),点P(x,y)在△ABC的边界及其 内部运动,则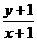的最大值为 　4　　 ,最小值为 　2.5　　 ．

14.已知三个球的半径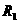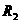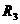，，满足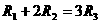，则它们的表面积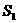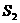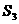，，，满足的等量关系是___________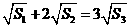

12.长方体的过一个顶点的三条棱长的比是1∶2∶3，对角线长为2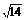，则这个长方体的体积是　 48　　

11.已知△ABC所在平面外一点P到△ABC三顶点的距离都相等,则P在平面△ABC内的射影是△ABC的 外心　　　

10．已知a,b,c是三条直线，且a∥ b，a与c的夹角为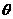，那么b与c夹角是　 　　　

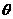
9．过点P(2,3),倾斜角为135°的直线的点斜式方程为　 y-3=-(x-2)